
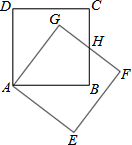
 如图,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF.
如图,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF. 分析 连结AH,如图,根据正方形的性质得AD=AB=BC=CD,∠B=∠D=90°,再根据旋转的性质得AG=AD,GF=CD,∠G=∠D=90°,于是可利用“HL”判断Rt△AGH≌△ABH,则GH=BH,所以BC-BH=GF-GH,即HC=HF.
解答 证明: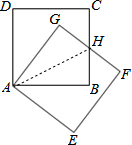 连结AH,如图,
连结AH,如图,
∵四边形ABCD为正方形,
∴AD=AB=BC=CD,∠B=∠D=90°,
∵正方形ABCD绕着点A按顺时针方向旋转得到正方形AEFG,
∴AG=AD,GF=CD,∠G=∠D=90°,
∴AG=AB,
在Rt△AGH和△ABH中,
$\left\{\begin{array}{l}{AH=AH}\\{AG=AB}\end{array}\right.$,
∴Rt△AGH≌△ABH,
∴GH=BH,
∴BC-BH=GF-GH,
即HC=HF.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
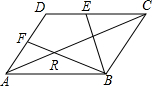 如图,在?ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,E,F分别为DC,DA的中点,求证:R为BF的三等分点.
如图,在?ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,E,F分别为DC,DA的中点,求证:R为BF的三等分点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一条公路修到湖边时,经过三次拐弯后,道路恰好与第一次拐弯之前的道路保持平行,如果第一次拐弯的角∠A=120°,第二次拐弯的角∠B=150°,则第三次拐弯的角∠C的度数等于150°.
如图,一条公路修到湖边时,经过三次拐弯后,道路恰好与第一次拐弯之前的道路保持平行,如果第一次拐弯的角∠A=120°,第二次拐弯的角∠B=150°,则第三次拐弯的角∠C的度数等于150°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
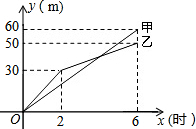 有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:
有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com