
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
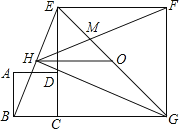
A. ①②③B. ①②④C. ①③④D. ②③④
【答案】A
【解析】
由四边形ABCD和四边形CGFE是正方形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得GH⊥BE;由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得HO∥BG且HO=![]() BG;由△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上,根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,从而证得△EHM∽△GHF;设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,由HO∥BG,得出△DHN∽△DGC,即可得出
BG;由△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上,根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,从而证得△EHM∽△GHF;设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,由HO∥BG,得出△DHN∽△DGC,即可得出![]() ,得到
,得到![]() ,即a2+2ab-b2=0,从而求得
,即a2+2ab-b2=0,从而求得![]() ,设正方形ECGF的边长是2b,则EG=2
,设正方形ECGF的边长是2b,则EG=2![]() b,得到HO=
b,得到HO=![]() b,通过证得△MHO△MFE,得到
b,通过证得△MHO△MFE,得到![]() ,进而得到
,进而得到![]() ,进一步得到
,进一步得到![]() .
.
解:如图,
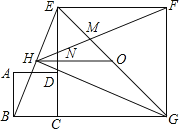
∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,
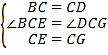
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①正确;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△GHF,
故②正确;
∵△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO∥BG,
∴△DHN∽△DGC,
![]()
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
![]()
即a2+2ab﹣b2=0,
解得:a=b=(﹣1+![]() )b,或a=(﹣1﹣
)b,或a=(﹣1﹣![]() )b(舍去),
)b(舍去),
![]()
![]()
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HO=![]() BG,
BG,
∴HO=![]() EG,
EG,
设正方形ECGF的边长是2b,
∴EG=2![]() b,
b,
∴HO=![]() b,
b,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO△MFE,
∴![]() ,
,
∴EM=![]() OM,
OM,
∴![]() ,
,
∴![]()
∵EO=GO,
∴S△HOE=S△HOG,
∴![]()
故④错误,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=20°,下列结论中正确的有( )①CE=OE②∠C=50° ③![]() =
=![]() ④AD=2OE
④AD=2OE
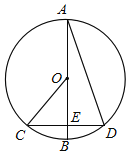
A.①④B.②③C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图l,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的点(与
上的点(与![]() ,
,![]() 不重合),
不重合),![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() .
.
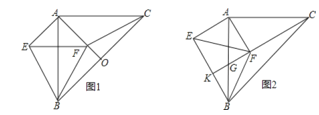
(1)求证:![]() ;
;
(2)如图2,若将![]() 绕点
绕点![]() 旋转,使边
旋转,使边![]() 在
在![]() 的内部,延长
的内部,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①求证:![]() ;
;
②当![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() 时,请求出
时,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
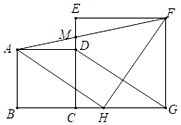
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
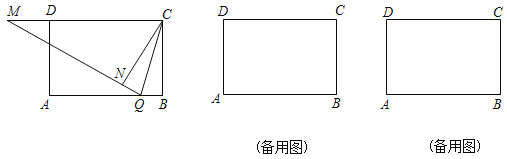
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,有一块含有30°的直角三角形![]() 的直角边
的直角边![]() 的长恰与另一块等腰直角三角形
的长恰与另一块等腰直角三角形![]() 的斜边
的斜边![]() 的长相等.把该套三角板放置在平面直角坐标系中,且
的长相等.把该套三角板放置在平面直角坐标系中,且![]()
(1)若某开口向下的抛物线的顶点恰好为点![]() ,请写出一个满足条件的抛物线的解析式.
,请写出一个满足条件的抛物线的解析式.
(2)若把含30°的直角三角形绕点![]() 按顺时针方向旋转后,斜边
按顺时针方向旋转后,斜边![]() 恰好与轴重叠,点
恰好与轴重叠,点![]() 落在点
落在点![]() ,试求图中阴影部分的面积(结果保留
,试求图中阴影部分的面积(结果保留![]() )
)
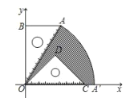
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程2x2﹣3x﹣6=0有两个实数根a,b,直线经过点A(a+b,0)和点B(0,ab),则直线l的函数表达式为( )
A.y=2x﹣3B.y=2x+3C.y=﹣2x+3D.y=﹣2x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,且关于直线
,且关于直线![]() 对称,
对称,![]() 是抛物线与x轴的一个交点.有下列结论:①方程
是抛物线与x轴的一个交点.有下列结论:①方程![]() 的一个根是x=-2;②若
的一个根是x=-2;②若![]() ,则
,则![]() ;③若
;③若![]() 时,方程
时,方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() ;④若
;④若![]() 时,
时,![]() ,则
,则![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com