
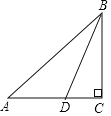
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
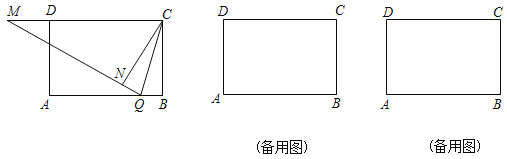
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
【答案】(1)见解析;(2)2.5;(3)![]() 或2
或2
【解析】
(1)由矩形的性质得出∠B=90°,AB=CD=6,CD∥AB,得出∠MCQ=∠CQB,由折叠的性质得出△CBQ≌△CNQ,求出BC=NC=4,NQ=BQ=1,∠CNQ=∠B=90°,∠CQN=∠CQB,得出∠CNM=90°,∠MCQ=∠CQN,证出MC=MQ.
(2)设DM=x,则MQ=MC=6+x,MN=5+x,在Rt△CNM中,由勾股定理得出方程,解方程即可.
(3)分两种情况:①当点M在CD延长线上时,由(1)得:∠MCQ=∠CQM,证出∠FDM=∠F,得出MD=MF,过M作MH⊥DF于H,则DF=2DH,证明△MHD∽△CED,得出![]() ,求出MD=
,求出MD=![]() CD=1,MC=MQ=7,由勾股定理得出MN即可解决问题.
CD=1,MC=MQ=7,由勾股定理得出MN即可解决问题.
②当点M在CD边上时,同①得出BQ=2即可.
(1)证明:∵四边形ABCD是矩形,
∴DC∥AB
即∠MCQ=∠CQB,
∵△BQC沿CQ所在的直线对折得到△CQN,
∴∠CQN=∠CQB,
即∠MCQ=∠MQC,
∴MC=MQ.
(2)∵四边形ABCD是矩形,△BQC沿CQ所在的直线对折得到△CQN,
∴∠CNM=∠B=90°,
设DM=x,则MQ=MC=6+x,MN=5+x,
在Rt△CNM中,MB2=BN2+MN2,
即(x+6)2=42+(x+5)2,
解得:x=![]() ,
,
∴DM=![]() ,
,
∴DM的长2.5.
(3)解:分两种情况:
①当点M在CD延长线上时,如图所示: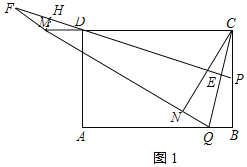
由(1)得∠MCQ=∠MQC,
∵DE⊥CQ,
∴∠CDE=∠F,
又∵∠CDE=∠FDM,
∴∠FDM=∠F,
∴MD=MF.
过M点作MH⊥DF于H,则DF=2DH,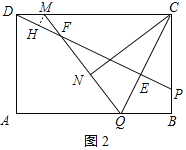
又![]() ,
,
∴![]() ,
,
∵DE⊥CQMH⊥DF,
∴∠MHD=∠DEC=90°,
∴△MHD∽△DEC
∴![]() ,
,
∴DM=1,MC=MQ=7,
∴MN=![]()
∴BQ=NQ=![]()
②当点M在CD边上时,如图所示,类似可求得BQ=2.
综上所述,BQ的长为![]() 或2.
或2.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P为AB延长线上一点,PC切⊙O于点C,过点B作BE∥PC交⊙O于点E,连接CE,CB.
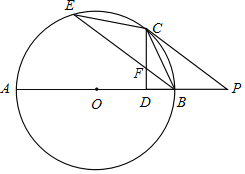
(1)试判断△BCE的形状,并说明理由;
(2)过点C作CD⊥AB于点D交BE于点F,若cosP=![]() ,CF=5,求AB的长.
,CF=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
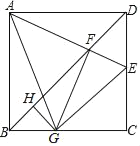
【题目】如图,正方形ABCD的边长为定值,E是边CD上的动点(不与点C,D重合),AE交对角线BD于点F,FG⊥AE交BC于点G,GH⊥BD于点H.现给出下列命题:①AF=FG;②FH的长度为定值.则( )
A.①是真命题,②是真命题B.①是真命题,②是假命题
C.①是假命题,②是真命题D.①是假命题,②是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
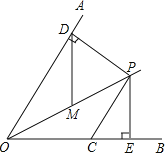
【题目】如图,已知OP平分∠AOB,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.CP=![]() ,PD=6.如果点M是OP的中点,则DM的长是_____.
,PD=6.如果点M是OP的中点,则DM的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
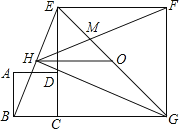
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
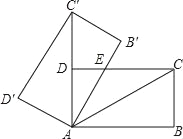
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线;以BC为直径的⊙O交BD于点E,连接CE并延长交AB于点F,连接DF,
(1)补全图中图形;(要求:清晰、准确,标出相应字母,不写作法,不必保留作图痕迹)
(2)DC=DF;
(3)若AC=8,BC=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com