
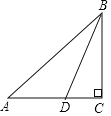
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线;以BC为直径的⊙O交BD于点E,连接CE并延长交AB于点F,连接DF,
(1)补全图中图形;(要求:清晰、准确,标出相应字母,不写作法,不必保留作图痕迹)
(2)DC=DF;
(3)若AC=8,BC=6,求CF的长.
【答案】(1)作图见解析;(2)证明见解析;(3)CF![]() .
.
【解析】
(1)由题意画出图形;
(2)通过证明△BEF≌△BEC,可得EF=CE,可得BD是CF的垂直平分线,即DF=CD;
(3)由勾股定理可求AB的长,CD的长,BD的长,由三角形面积公式可求CE的长,即可求CF的长.
(1)如图,
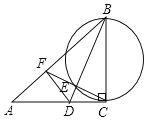
(2)∵BC是直径,
∴∠CEB=90°.
∵BD平分∠CBF,
∴∠FBD=∠CBD,且BD=BD,∠CEB=∠BEF=90°,
∴△BEF≌△BEC(ASA),
∴EF=CE,且BD⊥CF,
∴BD是CF的垂直平分线,
∴DF=CD
(3)∵AC=8,BC=6,
∴AB![]()
![]() 10.
10.
∵△BEF≌△BEC,
∴BF=BC=6,
∴AF=4,
∵BD是CF的垂直平分线,即点C、点F关于直线BD对称,
∴∠BFD=∠BCD=90°,
∴∠AFD=90°,
在Rt△AFD中,AD2=AF2+DF2,
∴(8﹣CD)2=16+CD2,
∴CD=3,
∴BD![]()
![]() 3
3![]()
∵S△BCD![]() BC×CD
BC×CD![]() BD×CE,
BD×CE,
∴3×6=3![]() CE,
CE,
∴CE![]() ,
,
∴CF=2CE![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】已知x2﹣8x+16﹣m2=0(m≠0)是关于x的一元二次方程
(1)证明:此方程总有两个不相等的实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c是该方程的两个实数根,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
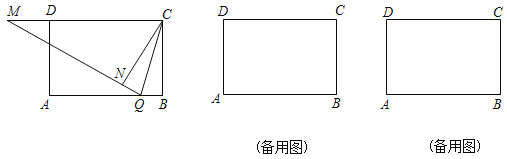
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
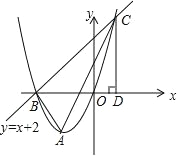
【题目】如图,已知抛物线 y=x2+2x 的顶点为 A,直线 y=x+2 与抛物线交于 B,C 两点.
(1)求 A,B,C 三点的坐标;
(2)作 CD⊥x 轴于点 D,求证:△ODC∽△ABC;
(3)若点 P 为抛物线上的一个动点,过点 P 作 PM⊥x 轴于点 M,则是否还存在除 C 点外的其他位置的点,使以 O,P,M 为顶点的三角形与△ABC 相似? 若存在,请求出这样的 P 点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程2x2﹣3x﹣6=0有两个实数根a,b,直线经过点A(a+b,0)和点B(0,ab),则直线l的函数表达式为( )
A.y=2x﹣3B.y=2x+3C.y=﹣2x+3D.y=﹣2x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
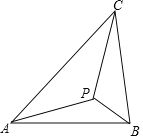
A.5 B.4 C.3+![]() D.2+
D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
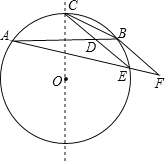
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1:![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令,某记者在一停车场对开车的司机进行了相关的调查,本次调查结果共有四种情况:①有时会喝点酒开车;②已戒酒或从不喝酒;③酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查情况整理并绘制成如下尚不完整的统计图,请根据相关信息,解答下列问题.
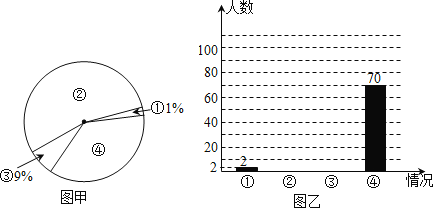
(1)该记者本次一共调查
了 名司机.
(2)求图①中④所在扇形的圆心角,并补全图②.
(3)在本次调查中,记者随机采访其中一名司机,求他属于第②种情况的概率.
(4)请估计在开车的10万名司机中,违反“酒驾”禁令的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
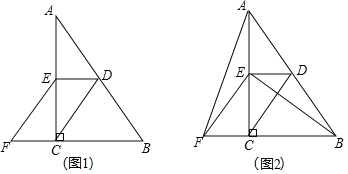
【题目】已知:如图,在![]() 中,
中,![]() ,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且
,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且![]() .
.
![]() 如图1,求证:四边形CDEF是平行四边形;
如图1,求证:四边形CDEF是平行四边形;
![]() 如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与
如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与![]() 面积相等的三角形.
面积相等的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com