
【题目】如图l,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的点(与
上的点(与![]() ,
,![]() 不重合),
不重合),![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() .
.
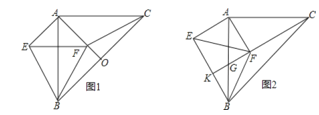
(1)求证:![]() ;
;
(2)如图2,若将![]() 绕点
绕点![]() 旋转,使边
旋转,使边![]() 在
在![]() 的内部,延长
的内部,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①求证:![]() ;
;
②当![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() 时,请求出
时,请求出![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)通过证明△EAB≌△FAB,即可得到BE=BF;
(2)①首先证明△AEB≌△AFC,由相似三角形的性质可得:∠EBA=∠FCA,进而可证明△AGC∽△KGB;
②根据题意,可分类讨论求值即可.
(1)∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF-∠BAF=45°,
∴∠EAB=∠BAF=45°,
在△EAB和△FAB中,
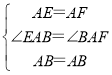 ,
,
∴△EAB≌△FAB(SAS),
∴BE=BF;
(2)①∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
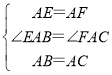 ,
,
∴△AEB≌△AFC(SAS),
∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,
∴△AGC∽△KGB;
②当∠EBF=90°时,
∵EF=BF,
∴∠FEB=∠EBF=90°(不符合题意),
当∠BEF=90°,且EF=BF时,
∴∠FEB=∠EBF=90°(不符合题意),
当∠EFB=90°,且EF=BF时,如下图,
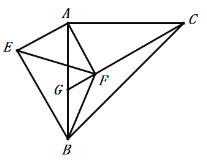
∴∠FEB=∠FBE=45°,
∵![]() ,
,![]() ,
,
∴∠AFE=∠AEF=45°,
∴∠AEB=∠AEF+∠FEB=45°+ 45°=90°,
不妨设![]() ,则BF= EF=
,则BF= EF=![]() ,BE=
,BE=![]() ,
,
在Rt△ABE中,∠AEB =90°,![]() ,BE
,BE![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是反比例函数![]() 的图象的一个分支.
的图象的一个分支.
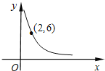
![]() 比例系数
比例系数![]() 的值是________;
的值是________;
![]() 写出该图象的另一个分支上的
写出该图象的另一个分支上的![]() 个点的坐标:________、________;
个点的坐标:________、________;
![]() 当
当![]() 在什么范围取值时,
在什么范围取值时,![]() 是小于
是小于![]() 的正数?
的正数?
![]() 如果自变量
如果自变量![]() 取值范围为
取值范围为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
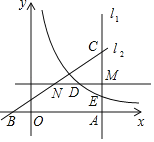
【题目】如图,直线l1经过点A(6,0),且垂直于x轴,直线l2:y=kx+b(b>0)经过点B(﹣2,0),与l1交于点C,S△ABC=16.点M是线段AC上一点,直线MN∥x轴,交l2于点N,D是MN的中点.双曲线y=![]() (x>0)经过点D,与l1交于点E.
(x>0)经过点D,与l1交于点E.
(1)求l2的解析式;
(2)当点M是AC中点时,求点E的坐标;
(3)当MD=1时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
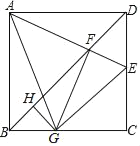
【题目】如图,正方形ABCD的边长为定值,E是边CD上的动点(不与点C,D重合),AE交对角线BD于点F,FG⊥AE交BC于点G,GH⊥BD于点H.现给出下列命题:①AF=FG;②FH的长度为定值.则( )
A.①是真命题,②是真命题B.①是真命题,②是假命题
C.①是假命题,②是真命题D.①是假命题,②是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a1,排在第二位的数称为第二项,记为a2,以此类推,排在第n位的数称为第n项,记为![]() .所以,数列的一般形式可以写成:
.所以,数列的一般形式可以写成:![]() ,…,
,…,![]() ,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:
,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:
(1)等差数列5,10,15,…的公差d为 ,第5项是 .
(2)如果一个数列![]() ,…,
,…,![]() ,…,是等差数列,且公差为d,那么根据定义可得到:
,…,是等差数列,且公差为d,那么根据定义可得到:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….所以
,….所以
![]()
![]()
![]()
……由此,请你填空完成等差数列的通项公式:![]() ( )d
( )d
(3)求-4039是等差数列-5,-7,-9,…的第几项?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
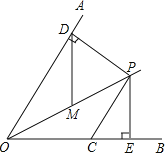
【题目】如图,已知OP平分∠AOB,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.CP=![]() ,PD=6.如果点M是OP的中点,则DM的长是_____.
,PD=6.如果点M是OP的中点,则DM的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
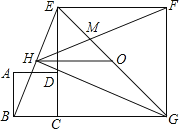
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
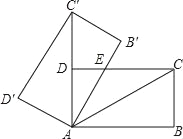
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
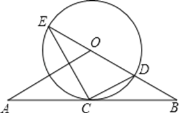
(1)求证:直线AB是⊙O的切线;
(2)试猜想BC,BD,BE三者之间的等量关系,并加以证明;
(3)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com