
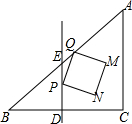
 如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).
如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).分析 (1)利用等腰直角三角形的性质即可;
(2)由正方形的性质得到△FPQ≌△GQM,用时间t表示线段建立方程即可;
(3)按时间分情况,利用面积之和或差表示出所求的图形的面积即可;
(4)找出整个运动过程中线段QM所扫过的面积和△AEM面积一样大即可.
解答 解:(1)∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∵DE∥AC,
∴∠FEQ=45°,
∵EQ=$\sqrt{2}$t,
∴QF=t,
故答案为t.
(2)过点Q作QF⊥DE交AC于G,如图1,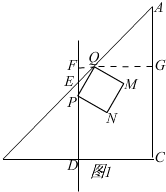
∵∠C=90°,DE⊥BC,
∴DE∥AC,
∴∠PFQ=∠QGM=90°,
∵四边形PQMN为正方形,
∴∠PQM=90°,PQ=MQ,
∴∠FPQ+∠FQP=∠FQP+∠GQM=90°,
∴∠FPQ=∠GQM..
∴△FPQ≌△GQM,
∴FP=GQ,
∵AC=BC=12,点D为BC中点,
∴∠A=∠B=45°,CD=6,
∵PT=EF=t,PF=QG=2t,
∴t+2t=6,
∴t=2;
解:(3)当正方形顶点落在BC边上时,如图2,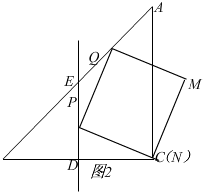
2(6-t)=6,
∴t=3,
当0<t≤2时,如图3,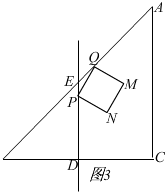
S=PQ2=t2+(2t)2=5t2,
当2<t≤3时,如图4,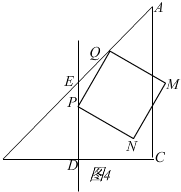
S=[$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$(6-t)]2=-$\frac{25}{4}$t2+45t-45,
当3<t≤6时如图5,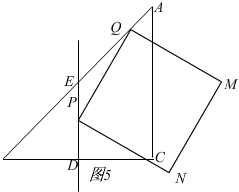
S=$\frac{1}{2}$(6+12)×6-$\frac{1}{2}$t2(6-t)2-$\frac{1}{4}$(6-t)2=-$\frac{9}{4}$t2+21t-9,
(4)解:如图6,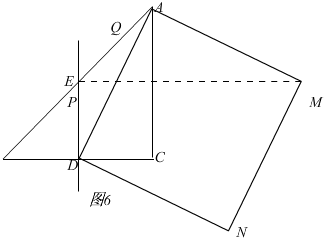
AC与MN的交点为H,由题意由EH=AH=6,△ACD≌△MHA,
∴MH=AC=6,∴EM=EH+MG=18,
∴S线段QM所扫过的面积=S△AEM=$\frac{1}{2}$×EM×AH=$\frac{1}{2}$×18×6=54.
点评 此题是四边形的综合题,主要考查动点中正方形随之变化的情景,解题的关键是分段来求图形的面积,本题的难点是重叠部分面积的计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一坡长AB为$70\sqrt{5}$,坡度i1=1:2的山顶B处修建一座铁塔BC,小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°,已知山坡AD的坡度i2=1:0.75
如图,在一坡长AB为$70\sqrt{5}$,坡度i1=1:2的山顶B处修建一座铁塔BC,小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°,已知山坡AD的坡度i2=1:0.75查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1×106米 | B. | 1×10-5米 | C. | 1×10-6米 | D. | 1×105米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
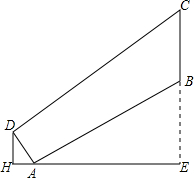
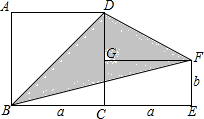 如图,正方形ABCD的边长为a,面积为6;长方形CEFG的长、宽分别为a,b,长方形的面积为2,其中点B、C、E在同一直线上,连接DF.求△BDF的面积.
如图,正方形ABCD的边长为a,面积为6;长方形CEFG的长、宽分别为a,b,长方形的面积为2,其中点B、C、E在同一直线上,连接DF.求△BDF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
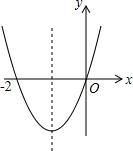 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2n;④am2+bn+a>0(a≠-1).其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}$ | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com