
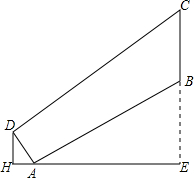
 如图,在一坡长AB为$70\sqrt{5}$,坡度i1=1:2的山顶B处修建一座铁塔BC,小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°,已知山坡AD的坡度i2=1:0.75
如图,在一坡长AB为$70\sqrt{5}$,坡度i1=1:2的山顶B处修建一座铁塔BC,小李在其对面山坡沿坡面AD向上走了25米到D处测得塔顶C的仰角为37°,已知山坡AD的坡度i2=1:0.75分析 (1)由AD的坡度i2=1:0.75,AD=25米,利用坡度的定义求即即可求得答案;
(2)首先过点D作DF⊥BC于点F,易得四边形DHEF是矩形,然后分别解Rt△ABE与Rt△DCF,继而求得答案.
解答 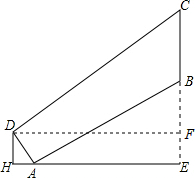 解:(1)∵AD的坡度i2=1:0.75,
解:(1)∵AD的坡度i2=1:0.75,
∴$\frac{DH}{AH}$=1:0.75=$\frac{4}{3}$,
∴$\frac{DH}{AD}$=$\frac{4}{5}$,
∵AD=25米,
∴DH=AD×$\frac{4}{5}$=20(米),
∴AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=15(米),
答:点D距水平面AE的高度DH=20米;
(2)过点D作DF⊥BC于点F,
∴∠DFE=90°,
∵∠H=∠E=90°,
∴四边形DHEF是矩形,
∴EF=DH=20米,DF=EH,
∵AB为$70\sqrt{5}$米,坡度i1=1:2,
∴$\frac{BE}{AE}$=$\frac{1}{2}$,
∴$\frac{BE}{AB}$=$\frac{1}{\sqrt{5}}$,
∴BE=70米,AE=140米,
∴DF=AH+AE=155(米),
∵∠CDE=37°,
∴CF=DF•tan37°=155×0.75=116.25(米),
∴BC=CF+EF-BE=116.25+15-70=61.25(米).
答:BC的高度为61.25米.
点评 此题考查了坡度坡角以及仰角俯角问题.注意准确构造直角三角形是解此题的关键.


科目:初中数学 来源: 题型:填空题
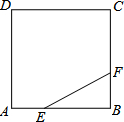 如图,正方形ABCD的边长为6,点E,F分别在边AB,BC上,AE=BF=2,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为12$\sqrt{5}$.
如图,正方形ABCD的边长为6,点E,F分别在边AB,BC上,AE=BF=2,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为12$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-9+6x=(x+3)(x-3)+6x | B. | (x+5)(x-2)=x2+3x-10 | ||
| C. | x2-8x+16=(x-4)2 | D. | -6a2b=-3a﹒2ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
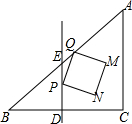 如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).
如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com