【题目】如图，Rt△ABC中，∠C=90°，∠A=30°．
（1）作线段AB的垂直平分线DE，垂足为点E，交AC于点D，要求用尺规作图，保留作图痕迹，标注有关字母，不要求写作法和证明；
（2）连接BD，直接写出∠CBD的度数；
（3）如果△BCD的面积为4，请求出△BAD的面积．

参考答案：

【答案】
（1）解：如图，DE为所作；


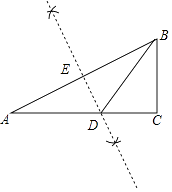
（2）解：∵DE垂直平分AB，

∴DA=DB，

∴∠DBA=∠A=30°，

∵∠ABC=90°﹣∠A=60°，

∴∠CBD=∠ABC﹣∠DBA=60°﹣30°=30°；


（3）解：在Rt△BCD中，∵∠CBD=30°，

∴DB=2CD，

而DA=DB，

∴DA=2CD，

∴S△ABD=2S△BCD=8．


【解析】（1）利用基本作图，作AB的垂直平分线即可；（2）利用垂直平分线的性质得DA=DB，则∠DBA=∠A=30°，然后计算∠ABC﹣∠DBA即可；（3）在Rt△BCD中利用含30度的直角三角形三边的关系得到DB=2CD，则DA=2CD，然后根据三角形面积公式得到S△ABD=2S△BCD=8．
【考点精析】关于本题考查的线段垂直平分线的性质，需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案．

关闭