
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.

【答案】(1)小亮与塔底中心的距离BD(1.9a﹣0.2)米;(2)慈氏塔的高度AB为36.1米.
【解析】
(1)由题意得,四边形CDBG、HBFE为矩形,求得GH=0.2,在Rt△AHE中,利用∠AEH的正切求得AH≈1.9a,从而得AG=1.9a﹣0.2,在Rt△ACG中,根据等腰直角三角形的性质求得CG=AG=1.9a﹣0.2,由此即可求得答案;
(2)由题意可得关于a的方程,解方程求得a的值即可得答案.
(1)由题意得,四边形CDBG、HBFE为矩形,
∴GB=CD=1.7,HB=EF=1.5,
∴GH=0.2,
在Rt△AHE中,tan∠AEH=![]() ,
,
则AH=HEtan∠AEH≈1.9a,
∴AG=AH﹣GH=1.9a﹣0.2,
在Rt△ACG中,∠ACG=45°,
∴CG=AG=1.9a﹣0.2,
∴BD=1.9a﹣0.2,
答:小亮与塔底中心的距离BD(1.9a﹣0.2)米;
(2)由题意得,1.9a﹣0.2+a=52,
解得,a=18,
则AG=1.9a﹣0.2=34.4,
∴AB=AG+GB=36.1,
答:慈氏塔的高度AB为36.1米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从共享单车、共享汽车等共享出行到共享充电宝、共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者,小宇上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),将这四张卡片背面朝上,洗匀放好.
(1)从中随机抽取一张,求刚好抽到“共享服务”的概率.
(2)从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
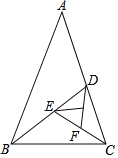
【题目】如图,等腰△ABC中,AB=AC,∠A=36°,作底角∠ABC的平分线BD交AC于点D,易得等腰△BCD,作等腰△BCD底角∠BCD的平分线CE,交BD于点E,得等腰△CDE,再作等腰△CDE底角∠CDE的平分线DF,交于CE于点F,…,若已知AB=b,BC=a,记△ABC为第一个等腰三角形,△BCD为第二个等腰三角形…,则![]() 的值为_____;第n个等腰三角形的底边长为_____.(含有b的代数式表示)
的值为_____;第n个等腰三角形的底边长为_____.(含有b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF。
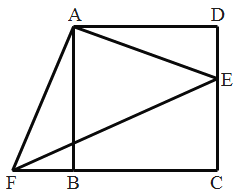
(1)求证:△ADE≌△ABF
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针方向旋转________度得到;
(3)若BC=8,DE=3,求△AEF的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )
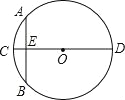
A.12寸 B.13寸 C.24寸 D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,给出如下定义:若点P的横、纵坐标均为整数,且到圆心C的距离d≤r,则称P为⊙C 的关联整点.
(1)当⊙O的半径r=2时,在点D(2,-2),E(-1,0),F(0,2)中,为⊙O的关联整点的是 ;
(2)若直线![]() 上存在⊙O的关联整点,且不超过7个,求r的取值范围;
上存在⊙O的关联整点,且不超过7个,求r的取值范围;
(3)⊙C的圆心在x轴上,半径为2,若直线![]() 上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com