
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
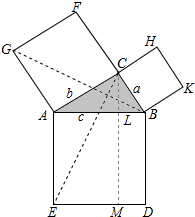 关于勾股定理,有很多证法,在我国它们都是用拼图形面积方法来证明的.下面的证法是欧几里得证法.如图所示.在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2.
关于勾股定理,有很多证法,在我国它们都是用拼图形面积方法来证明的.下面的证法是欧几里得证法.如图所示.在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com