
 如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1B2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,B3的坐标为(6,2$\sqrt{3}$);点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).
如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1B2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,B3的坐标为(6,2$\sqrt{3}$);点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2). 分析 根据等边三角形的性质和∠B1OA2=30°,可求得∠B1OA2=∠A1B1O=30°,可求得OA2=2OA1=2,同理可求得OAn=2n-1,再结合含30°角的直角三角形的性质可求得△AnBnAn+1的边长,进一步可求得点Bn的坐标.
解答 解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠B1OA2=30°,
∴∠B1OA2=∠A1B1O=30°,可求得OA2=2OA1=2,
同理可求得OAn=2n-1,
∵∠BnOAn+1=30°,∠BnAnAn+1=60°,
∴∠BnOAn+1=∠OBnAn=30°
∴BnAn=OAn=2n-1,
即△AnBnAn+1的边长为2n-1,则可求得其高为$\frac{\sqrt{3}}{2}$×2n-1=$\sqrt{3}$×2n-2,
∴点Bn的横坐标为$\frac{1}{2}$×2n-1+2n-1=$\frac{3}{2}$×2n-1=3×2n-2,
∴点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2),点B3的坐标为(6,2$\sqrt{3}$).
故答案为:(6,2$\sqrt{3}$);(3×2n-2,$\sqrt{3}$×2n-2),
点评 本题主要考查等边三角形的性质和含30°角的直角三角形的性质,根据条件找到等边三角形的边长和OA1的关系是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
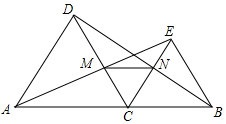 如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A在x轴正半轴上,点C在y轴正半轴上,OA=2OC,将矩形OABC绕原点O逆时针旋转90°,得到矩形ODEF.抛物线y=ax2+bx+c经过F、D、B三个点,其顶点在直线y=$\frac{7}{2}$x-$\frac{1}{12}$上,直线L:y=kx+m经过点E和点A,点P是抛物线y=ax2+bx+c上第一象限任意一点,过点P作x轴的垂线交直线L于点M.
如图,点A在x轴正半轴上,点C在y轴正半轴上,OA=2OC,将矩形OABC绕原点O逆时针旋转90°,得到矩形ODEF.抛物线y=ax2+bx+c经过F、D、B三个点,其顶点在直线y=$\frac{7}{2}$x-$\frac{1}{12}$上,直线L:y=kx+m经过点E和点A,点P是抛物线y=ax2+bx+c上第一象限任意一点,过点P作x轴的垂线交直线L于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
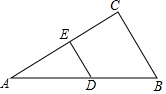 如图,在△ABC中,AB=8,∠C=90°,∠A=30°,D、E分别为AB、AC边上的中点,则DE的长为( )
如图,在△ABC中,AB=8,∠C=90°,∠A=30°,D、E分别为AB、AC边上的中点,则DE的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com