
【题目】如图,AD是△ABC的中线,tanB=![]() ,cosC=
,cosC=![]() ,AC=
,AC=![]()

(1)求BC的长;
(2)作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.
【答案】(1)5;(2)AO=![]() .
.
【解析】
(1)过点A作AE⊥BC于点E,根据三角函数的定义和特殊角的三角函数即可得出.
(2)作AB、AC的垂直平分线,交点O即为圆心,以0A为半径作圆,即可得出△ABC的外接圆,根据sin∠ABC=sin∠AOK即可求解.
解:(1)如图过点A作AE⊥BC于点E,

∵cosC=![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=![]() ,即
,即![]() ,
,
∴BE=4AE=4,
∴BC=BE+CE=5.
(2)如图,⊙O就是所求作的△ABC的外接圆.
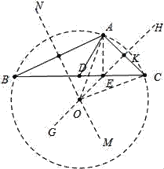
∵∠AOC=2∠ABC,∠AOK=∠COK,∴∠ABC=∠AOK,
∵sin∠AOK=sin∠ABC=![]()
由(1)可知AB=![]()
∴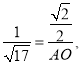
∴AO=![]() .
.


科目:初中数学 来源: 题型:
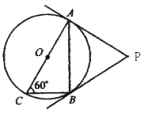
【题目】如图,AC是⊙0的直径,∠ACB=60°,连接AB,过A,B两点分别作⊙O的切线,两切线交于点P.若已知⊙0半径为1,则△PAB的周长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.

①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ,CD平分
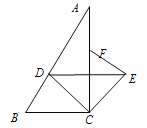
,CD平分![]() 交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
(1)△CDB旋转了________度;
(2)连结DE,判断DE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x元/件满足一次函数的关系,部分数据如下表:(![]() ,物价部门规定售价不得高于80元)
,物价部门规定售价不得高于80元)
销售单价x(元/件) | … | 55 | 60 | 65 | 70 | 75 |
一周的销售量y(件) | … | 450 | 400 | 350 | 300 | 250 |
(1)直接写出y与x的函数关系式:______;
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并求出销售利润的最大值;
(3)该商家要使每周的销售利润不低于5000元,那么销售单价应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+x+2=0;②3(x﹣9)2﹣(x+1)2=1;③x+3=![]() ;④(a2+a+1)x2﹣a=0;⑤
;④(a2+a+1)x2﹣a=0;⑤![]() =x﹣1.一元二次方程的个数是( )
=x﹣1.一元二次方程的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com