练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用反证法证明：“△ABC中至少有两个锐角”，第一步假设为____________________．

    【答案】△ABC中至多有一个锐角

    【解析】

    熟记反证法的步骤，直接填空即可．

    解：用反证法证明同一三角形中至少有两个锐角时，第一步应假设同一三角形中至多有一个锐角．

    故答案为：△ABC中至多有一个锐角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一个三角形的三条边长均为正整数.若其中仅有一条边长为5，且它不是最短边，则满足条件的三角形个数为________________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：a﹣b，x﹣y，x+y，a+b，x2﹣y2 ， a2﹣b2分别对应下列六个字：华、爱、我、中、游、美，现将（x2﹣y2）a2﹣（x2﹣y2）b2因式分解，结果呈现的密码信息可能是（ ）
    A.我爱美
    B.中华游
    C.爱我中华
    D.美我中华

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个人从A地出发向北偏东80°方向到达B地，再从B地向北偏西25°方向到达C地，如果∠ACB=55°，则∠CAB的度数是（　　）

    A. 25° B. 50° C. 70° D. 75°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

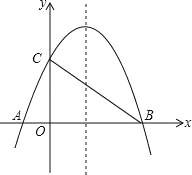
    【题目】如图，已知抛物线y=-x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知B点的坐标为B（8，0）．

    （1）求抛物线的解析式及其对称轴方程；

    （2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由；

    （3）M为抛物线上BC之间的一点，N为线段BC上的一点，若MN∥y轴，求MN的最大值；

    （4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】4月24日6时到11时某城市空气质量指数PM2.5的1小时均值（单位：μg/m3）如下：70，74，78，80，74，75，这组数据中位数和众数分别是（ ）

    A. 79和74 B. 74.5和74 C. 74和74.5 D. 74和79

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】尺规作图作一个角的角平分线的依据是（　 　）．

    A. SASB. ASAC. AASD. SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果点A（5，y）在x轴的上方，则y的取值范围为（ ）

    A. 小于0 B. 大于0 C. 大于等于0 D. 小于或等于0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果点P（m+1，m+3）在y轴上，则m=_____．

    查看答案和解析>>

    同步练习册答案