
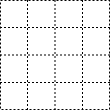
 如图是由16个边长为1的小正方形组成的格点图形,任意连接这些小正方形的若干个顶点,可以得到一些线段,试在图中分别画出两条有理数的线段和两条长度为无理数的线段,并说明理由.
如图是由16个边长为1的小正方形组成的格点图形,任意连接这些小正方形的若干个顶点,可以得到一些线段,试在图中分别画出两条有理数的线段和两条长度为无理数的线段,并说明理由.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
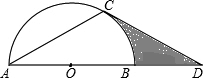 如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
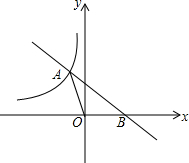 图中曲线是反比例函数y=$\frac{n+7}{x}$的图象的一支.
图中曲线是反比例函数y=$\frac{n+7}{x}$的图象的一支.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com