
【题目】已知抛物线y=![]() -(x-m),其中m是常数.
-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=![]()
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
【答案】(1)证明见解析;(2)y=x2-5x+6;平移![]() 个单位长度.
个单位长度.
【解析】试题分析:(1)先把抛物线解析式化为一般式,再计算△的值,得到△=1>0,于是根据△=b2-4ac决定抛物线与x轴的交点个数即可判断不论m为何值,该抛物线与x轴一定有两个公共点;
(2)①根据对称轴方程得到=-![]() ,然后解出m的值即可得到抛物线解析式;
,然后解出m的值即可得到抛物线解析式;
②根据抛物线的平移规律,设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2-5x+6+k,再利用抛物线与x轴的只有一个交点得到△=52-4(6+k)=0,然后解关于k的方程即可.
试题解析:(1)y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,
∵△=(2m+1)2-4(m2+m)=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)①∵x=-![]() ,
,
∴m=2,
∴抛物线解析式为y=x2-5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2-5x+6+k,
∵抛物线y=x2-5x+6+k与x轴只有一个公共点,
∴△=52-4(6+k)=0,
∴k=![]() ,
,
即把该抛物线沿y轴向上平移![]() 个单位长度后,得到的抛物线与x轴只有一个公共点.
个单位长度后,得到的抛物线与x轴只有一个公共点.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位老师分别教数学、物理、化学、生物、语文和历史,每位老师教两门课程.化学老师和数学老师住在一起;甲老师最年轻;数学老师和丙老师爱下象棋;物理老师比生物老师年长,比乙老师年轻三人中最年长的老师住的地方比其他两位老师远.三位老师分别教哪两门课程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数n | 8 | 10 | 15 | 20 | 30 | 40 | 50 |
进球次数m | 6 | 8 | 12 | 17 | 25 | 32 | 40 |
进球频 |
(1)计算并填写进球频率.
(2)这位运动员投篮一次,进球的概率约是多少(精确到0.1)?
(3)这位运动员投篮十次,必定会投进八球吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然发生事件的是( )
A. 打开电视机,正在转播足球比赛
B. 小麦的亩产量一定为1000公斤
C. 在只装有5个红球的袋中摸出1球,是红球
D. 农历十五的晚上一定能看到圆月
查看答案和解析>>
科目:初中数学 来源: 题型:
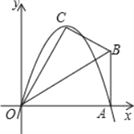
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com