
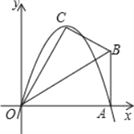
����Ŀ����֪��Rt��OAB��,��OAB=90��,��BOA=30��,AB=2.����OΪ����ԭ��,OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ,��B�ڵ�һ������.��Rt��OAB��OB�۵���,��A���ڵ�һ�����ڵĵ�C����
��1�����C�����ꣻ
��2����������y=ax2+bx��a��0������C��A���㣬��������ߵĽ���ʽ��
��3���������ߵĶԳ�����OB���ڵ�D,��PΪ�߶�DB��һ��,��P��y���ƽ����,���������ڵ�M����:�Ƿ���������ĵ�P,ʹ���ı���CDPMΪ�������Σ�������,�������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1����![]() ��3����2��
��3����2��![]() ��3�����ڣ���
��3�����ڣ��� ![]() ��
�� ![]() ��
��
���������⣺��1����C��CH��OA��H��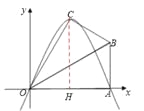
����Rt��OAB����OAB=90������BOA=30����AB=2����OA=![]() ��
��
����Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����
��OC=OA=![]() ����AOC=60����
����AOC=60����
��OH=![]() ��CH="3" ��
��CH="3" ��
��C�������ǣ�![]() ��3����
��3����
��2����������![]() ����C��
����C��![]() ��3����A��
��3����A��![]() ��0�����㣬
��0�����㣬
��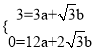 �����
�����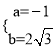 �����������ߵĽ���ʽΪ
�����������ߵĽ���ʽΪ![]()
��3�����ڡ�
��![]() �Ķ�������Ϊ��
�Ķ�������Ϊ��![]() ��3������Ϊ��C��
��3��������C��
MP��x�ᣬ�费��ΪN��PN��t��
�ߡ�BOA��300������ON��![]()
��P��![]() ��
��
��PQ��CD������ΪQ��ME��CD������ΪE��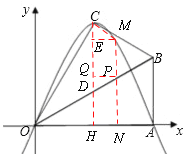
��![]() ����
����![]() �ã�
�ã� ![]() ��
��
�� M��![]() ��
�� ![]() ����E��
����E��![]() ��
�� ![]() ����
����
ͬ����Q��![]() ��t����D��
��t����D��![]() ��1����
��1����
Ҫʹ�ı���CDPMΪ�������Σ�ֻ��CE��QD��
��![]() ����ã�
����ã� ![]() ��
�� ![]() ����ȥ����
����ȥ����
�� P��������![]() ��
�� ![]() ����
����
�� �������������ĵ�P��ʹ���ı���CDPMΪ�������Σ���ʱP�����Ϊ��![]() ��
�� ![]() ����
����
��1����C��CH��OA��H�������۵��õ�OC=OA=4����A0C=60�������OH��CH���ɡ�
��2����C��![]() ��3����A��
��3����A��![]() ��0������
��0������![]() �õ������飬���������Ľ⼴�ɡ�
�õ������飬���������Ľ⼴�ɡ�
��3����ͼ�����ݵ������ε��ж���ֻҪCE��QD���ɣ��ݴ���ʽ��⡣


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ��������ǣ� ��
A.�й���������������ǶԶ���
B.����ʽx2��4x��ʽ�ֽ�Ľ����x��x2��4��
C.a+a=a2
D.һԪ���η���x2��x+2=0��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AOBC��ֱ������ϵ�У���A��y���ϣ���B��x���ϣ���֪��C�������ǣ�8��4����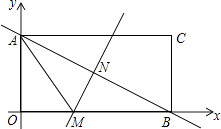
��1����Խ���AB����ֱ�ߵĺ�����ϵʽ��
��2���Խ���AB�Ĵ�ֱƽ����MN��x���ڵ�M������AM�����߶�AM�ij���
��3������P��ֱ��AB�ϵ�һ�����㣬����PAM������볤����OABC��������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=![]() -��x-m��������m�dz�����
-��x-m��������m�dz�����
��1����֤������mΪ��ֵ������������x��һ�������������㣻
��2�����������ߵĶԳ���Ϊֱ��x=![]()
����������ߵĺ�������ʽ��
���Ѹ���������y������ƽ�ƶ��ٸ���λ���Ⱥõ�����������x��ֻ��һ�������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�D��E��BC���ϵĵ㣬BD��DE��EC=3��2��1��M��AC���ϣ�CM��MA=1��2��BM��AD��AE��H��G����BH��HG��GM���ڣ� ��

A. 4��2��1 B. 5��3��1 C. 25��12��5 D. 51��24��10
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com