
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪OΪԭ�㣬�ı���ABCDΪƽ���ı��Σ�A��B��C������ֱ���A����5��1����B����2��4����C��5��4������D�ڵ�һ���ޣ� 
��1��д��D������ꣻ
��2����B��D�����ֱ�ߵĽ���ʽ�������߶�BD�ij���
��3����ƽ���ı���ABCD������ƽ��1����λ���ȣ�������ƽ��1����λ�������õ��ı���A1B1C1D1�ĸ�����������Ƕ��٣������ƽ���ı���ABCD���ı���A1B1C1D1�ص����ֵ������
���𰸡�
��1���⣺��B����2��4����C��5��4����
��BC=5������2��=5+2=7��
��A����5��1����
���D�ĺ�����Ϊ��5+7=2��
���D��������2��1����
��2���⣺��ֱ��BD�Ľ���ʽΪy=kx+b��
��B����2��4����D��2��1������ã� ![]() ��
��
��� 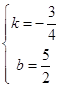 ��
��
�ྭ��B��D�����ֱ�ߵĽ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
��B����AD�Ĵ��ߣ�����ΪE����BE=4��1=3��

DE=2������2��=2+2=4��
��Rt��BDE��BD= ![]() =
= ![]() =5��
=5��
��3���⣺��ABCD����ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ�
��A1����4��0����B1����1��3����C1��6��3��D1��3��0����
���ص����ֵĵױ߳�7��1��1=5��
��Ϊ3��1=2��
���ص����ֵ����S=5��2=10��
����������1�����ݵ�B��C���������BC�ij��ȣ��ٸ���ƽ���ı��εĶԱ������ʽ�����D�ĺ����꣬Ȼ��д��D�����꼴�ɣ���2����ֱ��BD�Ľ���ʽΪy=kx+b��Ȼ�����ô���ϵ������һ�κ�������ʽ��𣻹���B��BE��AD��E�����BE��DE�ij���Ȼ�����ù��ɶ�����ʽ���㼴�ɵý⣻��3����������ƽ�ƺ�����ӣ�����ƽ������������A1��B1��C1��D1�����꣬Ȼ������ص�����ƽ���ı��εĵױߺߣ��ٸ���ƽ���ı��ε������ʽ��ʽ���㼴�ɵý⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD����AB��DC����ABC��90������A��45����AB��30��BC��x������15<x<30.����D��DE��AB�ڵ�E������ADE��ֱ��DE�۵���ʹ��A���ڵ�F����DF��BC�ڵ�G.

(1)�ú�x�Ĵ���ʽ��ʾBF�ij���
(2)���ı���DEBG�����ΪS����S����x�ĺ�������ʽ��
(3)��xΪ��ֵʱ��S�����ֵ�������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����߶Σ��ڵȱ������Σ��������Σ���Բ�����м�����Գ��������ĶԳƵ�ͼ���ǣ� ��
A.�٢ڢ�B.�ڢۢ�C.�٢ۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽���꼶��ѧ����ĩ������ѧ�ɼ����Ӿ��꼶ѧ���������ȡ�˲���ѧ�����е��飬��������ȡ��ѧ����ѧ�ɼ����ɼ���Ϊ��������ΪA��B��C��D��E����ȼ���A��50.5��60.5��B��60.5��70.5��C��70.5��80.5��D��80.5��90.5��E��90.5��100.5������������ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ����������⣺ 
��1����γ������鹲��ȡ�˶�����ѧ����
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������ĩ������ѧ�ɼ�����λ�������ĸ��ȼ��ڣ�
��4����У���꼶��800��ѧ�������涨80�����ϣ�����80�֣�Ϊ���ã��Թ��ƾ��꼶�ж�����ѧ������ѧ�ɼ�Ϊ���ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ1800m2����������̻������żס����������̶���ɣ���֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ400m2������̻�ʱ���ӱ��Ҷ�����4�죮
��1����ס��������̶�ÿ��������̻�������ֱ��Ƕ���m2��
��2����ѧУÿ���踶���ӵ��̻�����Ϊ0.4��Ԫ���Ҷ�Ϊ0.25��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����8��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com