练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若2m=3，4n=8，则23m﹣2n+3的值是

    【答案】27
    【解析】解：∵2m=3，4n=8，
    ∴23m﹣2n+3=（2m）3÷（2n）2×23 ，
    =（2m）3÷4n×23 ，
    =33÷8×8，
    =27．
    所以答案是：27．
    根据同底数幂的除法，幂的乘方的性质的逆运用先表示成已知条件的形式，然后代入数据计算即可．
    【考点精析】本题主要考查了同底数幂的除法的相关知识点，需要掌握同底数幂的除法法则：am÷an=am-n（a≠0，m，n都是正整数，且m＞n）才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y=x+3的图象与x、y轴交于A、B两点．直线l经过原点，与线段AB交于点C，把△AOB的面积分为2：1的两部分．求直线l的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某储运站现有甲种货物1530吨，乙种货物1150吨，安排用一列货车将这批货物运往外地，这列货车持A．B两种类型的货厢共50节。已知甲种货物35吨和乙种货物15吨可装满一节A型货厢，甲种货物25吨和乙种货物35吨可装满一节B型货厢，问：该储运站需配置A．B两种类型的货厢各几节？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列等式一定成立的是（　　）
    A.aa2=a2
    B.a2÷a=2
    C.2a2+a2=3a4
    D.（﹣a）3=﹣a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知抛物线y=﹣x2+2x经过原点O,且与直线y=x﹣2交于B，C两点．

    （1）求抛物线的顶点A的坐标及点B,C的坐标；

    （2）求证：∠ABC=90°；

    （3）在直线BC上方的抛物线上是否存在点P,使△PBC的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；

    （4）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

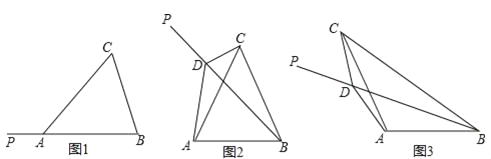
    【题目】如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）

    （1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD ∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是 ；

    （2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=AD；

    （3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，一辆汽车在直线形的公路AB上由A向B行驶，C，D分别是位于公路AB两侧的村庄.

    (1)该汽车行驶到公路AB上的某一位置C′时距离村庄C最近，行驶到D′位置时，距离村庄D最近，请在公路AB上作出C′，D′的位置(保留作图痕迹)；

    (2)当汽车从A出发向B行驶时，在哪一段路上距离村庄C越来越远，而离村庄D越来越近？(只叙述结论，不必说明理由)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣5，1），B（﹣2，4），C（5，4），点D在第一象限．
    （1）写出D点的坐标；
    （2）求经过B、D两点的直线的解析式，并求线段BD的长；
    （3）将平行四边形ABCD先向右平移1个单位长度，再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列每组数分别是三根木棒的长度，用它们能摆成三角形的是（ ）

    A.4cm，4cm，9cmB.3cm，5cm，8cm

    C.3cm，4cm，5cmD.1cm，2cm，3cm

    查看答案和解析>>

    同步练习册答案