
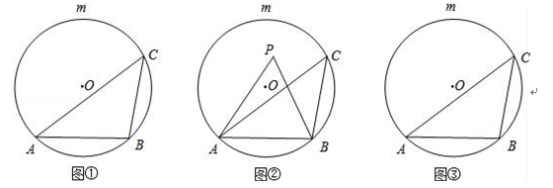
【题目】如图①,AB是⊙O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)若∠ACB=45°,点P是⊙O上一点(不与A、B重合),则∠APB= ;
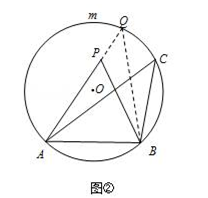
(2)如图②,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
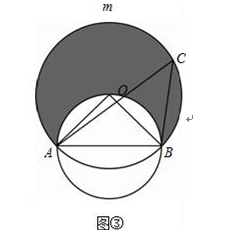
(3)请在图③中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
【答案】(1)45°或135°;(2)∠APB>∠ACB;(3)图见解析
【解析】
试题分析:(1)根据题意可知,存在两种情况,针对两种情况,可以画出相应的图形,由题目中的信息和同弧所对的圆周角相等,圆内接四边形对角互补,可以分别求得两种情况下∠APB的度数,本题得以解决;
(2)根据题意画出相应的图形,根据三角形的外角大于任何一个和它不相邻的内角,可以证明结论成立,本题得以解决;
(3)根据题意和第(2)问,可以画出满足∠ACB<∠APB<2∠ACB的点P所在的范围,本题得以解决.
试题解析:(1)解:如图①所示,

根据题意可分两种情况,
第一种情况,当点P在P1时,
可知,∠AP1B=∠ACB=45°;
第二种情况,当点P在P2时,
∵四边形ACBP2是圆内接四边形,
∴∠AP2B+∠ACB=180°,
∵∠ACB=45°,
∴∠AP2B=135°,
故答案为:45°或135°;
(2)证明:如下图②所示,延长AP交⊙O于点Q,连接BQ.
则∠PQB=∠ACB,
∵∠APB为△PQB的一个外角,
∴∠APB>∠PQB,
即∠APB>∠ACB;
(3)点P所在的范围如下图③所示,


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用等式的性质解方程的步骤:
(1)利用等式的性质________,方程两边同时加(或减)同一个数(或式子)使一元一次方程左边是________,右边是________;
(2)利用等式的性质________,方程两边同时乘未知数的系数的________,使未知数的系数化为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果基地积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击测试,每人20次射击的平均成绩恰好相等,且他们的标准差分别是S甲=1.8,S乙=0.7.在本次射击测试中,甲、乙两人中成绩较为稳定的是_____.(填:甲或乙)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的对话。
小红:“售货员,我要买些梨。”
售货员说:“小红,你上次买的那种梨卖完了,我们还没来得及进货,我建议你这次买些新进的苹果,价格比梨贵一点,不过这批苹果的味道挺好哟!”
小红:“好,这次和上次一样,也花30元。”
对照前后两次的电脑小票,小红发现,每千克苹果的单价是梨的1.5倍,买的苹果的重量比梨轻2.5Kg。
试根据上面的对话和小红的发现,分别求出苹果和梨的单价。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com