
【题目】光明社区为了调查居民对社区服务的满意度,随机抽取了社区部分居民进行问卷调查;用![]() 表示“很满意”,
表示“很满意”,![]() 表示“满意”,
表示“满意”,![]() 表示“比较满意”,
表示“比较满意”,![]() 表示“不满意”,如图是根据问卷调查统计资料绘制的两幅不完整的统计图.
表示“不满意”,如图是根据问卷调查统计资料绘制的两幅不完整的统计图.
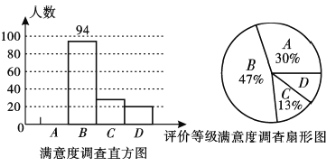
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查共调查了多少个居民?
(2)求出调查结果为![]() 的人数,并将直方图中
的人数,并将直方图中![]() 部分的图形补充完整;
部分的图形补充完整;
(3)如果该社区有居民5000人,请你估计对社区服务感到“不满意”的居民约有多少人?
科目:初中数学 来源: 题型:
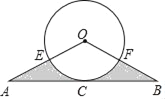
【题目】如图,在△AOB中,OA=OB,点C为AB的中点,AB=16,以点O为圈心,6为半径的圆经过点C,分别交OA、OB于点E、F.
(1)求证:AB为⊙O的切线;
(2)求图中阴影部分的面积.(注:结果保留π,sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员推铅球,铅球运行时离地面的高度![]() (米)是关于运行时间
(米)是关于运行时间![]() (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为![]() 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
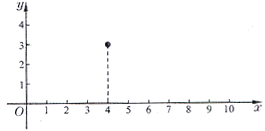
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似地,可以在等腰三角形中建立边角之间的关系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad)如图1,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad![]() .容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解答下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解答下列问题:
(1)sad![]() = ;
= ;
(2)对于![]() <A<
<A<![]() ,∠A的正对值sadA的取值范围 ;
,∠A的正对值sadA的取值范围 ;
(3如图2,已知sinA=![]() ,其中∠A为锐角,试求sadA的值。
,其中∠A为锐角,试求sadA的值。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
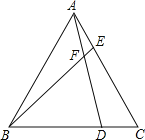
【题目】 如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD = AE,AD与BE相交于点F.
(1)求证:AD = BE;
(2)求∠BFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
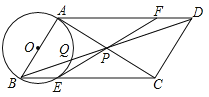
【题目】如图,在ABCD中,∠BAC=90°,对角线AC,BD相交于点P,以AB为直径的⊙O分别交BC,BD于点E,Q,连接EP并延长交AD于点F.
(1)求证:EF是⊙O的切线;
(2)求证:![]() =4BPQP.
=4BPQP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:将矩形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到矩形
得到矩形![]() .
.
(1)如图![]() ,当点
,当点![]() 在
在![]() 上时,求证:
上时,求证:![]()
(2)当旋转角![]() 的度数为多少时,
的度数为多少时,![]() ?
?
(3)若![]() ,请直接写出在旋转过程中
,请直接写出在旋转过程中![]() 的面积的最大值.
的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是正方形, G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.给出以下结论:①△AED≌△BFA;②DE﹣BF=EF;③△BGF∽△DAE;④DE﹣BG=FG.其中正确的有( )
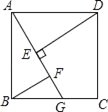
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com