
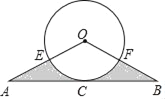
【题目】如图,在△AOB中,OA=OB,点C为AB的中点,AB=16,以点O为圈心,6为半径的圆经过点C,分别交OA、OB于点E、F.
(1)求证:AB为⊙O的切线;
(2)求图中阴影部分的面积.(注:结果保留π,sin37°=0.6,cos37°=0.8,tan37°=0.75)
科目:初中数学 来源: 题型:
【题目】今年10月某服装店老板用15000元购得“衬衣”和“T恤”共200件,其中“衬衣”和“T恤”的数量比为3:2,已知每件“衬衣”的售价比每件“T恤”的售价的2倍少20元,预计10月可全部售完.
(1)该批发商想通过本次销售共获利1800元,则每件“衬衣”卖多少元?
(2)实际销售时,受中央“厉行节约”号召的影响,在(1)中销售价的基础之上,“衬衣”的销售量不变,售价下降了a%,“T恤”的销售量下降了2a%,但售价不变,结果“衬衣”比“T恤”的销售额至少多了6480元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 ![]() cm?
cm?
(3)经过几秒,![]() 的面积等于
的面积等于![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径为6,则GE+FH的最大值为( )
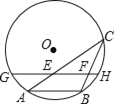
A. 6 B. 9 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
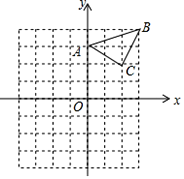
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明社区为了调查居民对社区服务的满意度,随机抽取了社区部分居民进行问卷调查;用![]() 表示“很满意”,
表示“很满意”,![]() 表示“满意”,
表示“满意”,![]() 表示“比较满意”,
表示“比较满意”,![]() 表示“不满意”,如图是根据问卷调查统计资料绘制的两幅不完整的统计图.
表示“不满意”,如图是根据问卷调查统计资料绘制的两幅不完整的统计图.
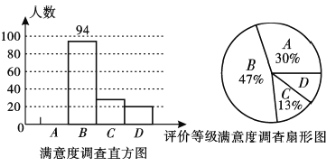
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查共调查了多少个居民?
(2)求出调查结果为![]() 的人数,并将直方图中
的人数,并将直方图中![]() 部分的图形补充完整;
部分的图形补充完整;
(3)如果该社区有居民5000人,请你估计对社区服务感到“不满意”的居民约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com