
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径为6,则GE+FH的最大值为( )
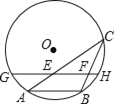
A. 6 B. 9 C. 10 D. 12
【答案】B
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为6,可得AB=OA=OB=6,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
解:如图,连接OA、OB,
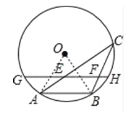 ,
,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵⊙O的半径为6,
∴AB=OA=OB=6,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=3,
AB=3,
要求GE+FH的最大值,即求GE+FH+EF(弦GH)的最大值,
∵当弦GH是圆的直径时,它的最大值为:6×2=12,
∴GE+FH的最大值为:12﹣3=9.
故选:B.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)直接写出OC=___________;
(2)如图1,当CP与⊙A相切时,求PO的长;
(3)如图2,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问当PO为何值时,△OCQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,设一次函数![]() 的图象是直线
的图象是直线![]() .
.
(1)如果把![]() 向下平移
向下平移![]() 个单位后得到直线
个单位后得到直线![]() ,求
,求![]() 的值;
的值;
(2)当直线![]() 过点
过点![]() 和点
和点![]() 时,且
时,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若坐标平面内有点![]() ,不论
,不论![]() 取何值,点
取何值,点![]() 均不在直线
均不在直线![]() 上,求
上,求![]() 所需满足的条件.
所需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级![]() 名学生的体育综合素质,随机抽查了
名学生的体育综合素质,随机抽查了![]() 名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图。
名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图。
频数分布表:
组别 | 成绩(分) | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请你根据以上图表提供的信息,解答下列问题:
(1)频数分布表中的![]() ;
;![]()
(2)扇形统计图中,![]() 组所对应的扇形圆心角的度数是_ 度.
组所对应的扇形圆心角的度数是_ 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,OA=OB,点C为AB的中点,AB=16,以点O为圈心,6为半径的圆经过点C,分别交OA、OB于点E、F.
(1)求证:AB为⊙O的切线;
(2)求图中阴影部分的面积.(注:结果保留π,sin37°=0.6,cos37°=0.8,tan37°=0.75)
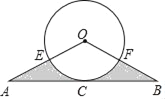
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他骑公共自行车比自驾车平均每小时少行驶45千米,他从家出发到上班地点,骑公共自行车所用的时间是自驾车所用的时间的4倍.小张骑公共自行车平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD = AE,AD与BE相交于点F.
(1)求证:AD = BE;
(2)求∠BFD的度数.
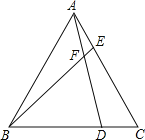
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com