
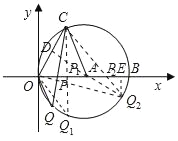
【题目】如图所示,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)直接写出OC=___________;
(2)如图1,当CP与⊙A相切时,求PO的长;
(3)如图2,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问当PO为何值时,△OCQ是等腰三角形?

【答案】(1)4;(2)4 (3)PO为2或2+2![]()
【解析】
(1)根据已知条件证明△AOC是等边三角形,由此即可求解;(2)根据切线的性质可得∠ACP=90°,在直角三角形APC中,即可得∠APC= 30°;有已知A点的坐标可得AC的长,即可求得PA的长,再由PO=PA-OA得出OP的值即可;(3)分OC=OQ和CQ=OQ两种情况求PO得值即可.
(1)∵∠AOC=60°,AO=AC,
∴△AOC是等边三角形,
∴OC=OA=4
(2)∵CP与⊙A相切,
∴∠ACP=90°,
∴∠APC=90°﹣∠OAC=30°;
又∵A(4,0),
∴AC=AO=4,
∴PA=2AC=8,
∴PO=PA﹣OA=8﹣4=4.
(3)①如图,过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;
∵OA是半径,
∴![]() ,
,
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=![]() OA=2;
OA=2;
②如图,过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2,
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=![]() ∠OAC=30°,
∠OAC=30°,
∴Q2E=![]() AQ2=2,AE=2
AQ2=2,AE=2![]() ,
,
∴点Q2的坐标(4+![]() ,﹣2);
,﹣2);
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴![]() ,
,
∴C点坐标(2,![]() );
);
设直线CQ2的关系式为y=kx+b,则
![]() ,
,
解得![]() ,
,
∴y=﹣x+2+2![]() ;
;
当y=0时,x=2+2![]() ,
,
∴P2O=2+2![]() ,
,
即:PO为2或2+2![]() 时,△OCQ是等腰三角形.
时,△OCQ是等腰三角形.


科目:初中数学 来源: 题型:
【题目】(10分)如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
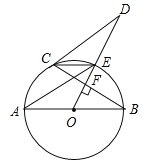
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
,![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙O 的半径是![]() ,
,
①求出⊙O上的所有梦之点的坐标;
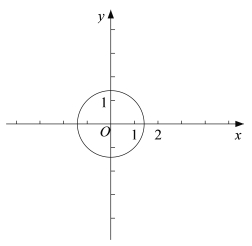
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
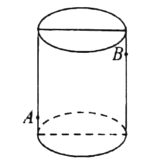
【题目】有一个圆柱形玻璃杯高![]() ,底面周长为
,底面周长为![]() ,有一只蚂蚁在一侧距下底
,有一只蚂蚁在一侧距下底![]() 的外侧
的外侧![]() 点,与点
点,与点![]() 正对的容器内侧距下底
正对的容器内侧距下底![]() 的
的![]() 点处有一饭粒,蚂蚁想吃
点处有一饭粒,蚂蚁想吃![]() 处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________
处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年10月某服装店老板用15000元购得“衬衣”和“T恤”共200件,其中“衬衣”和“T恤”的数量比为3:2,已知每件“衬衣”的售价比每件“T恤”的售价的2倍少20元,预计10月可全部售完.
(1)该批发商想通过本次销售共获利1800元,则每件“衬衣”卖多少元?
(2)实际销售时,受中央“厉行节约”号召的影响,在(1)中销售价的基础之上,“衬衣”的销售量不变,售价下降了a%,“T恤”的销售量下降了2a%,但售价不变,结果“衬衣”比“T恤”的销售额至少多了6480元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() ,
,![]() (或它们的延长线)于点
(或它们的延长线)于点![]() ,
,![]() 。当
。当![]() 绕点
绕点![]() 旋转到
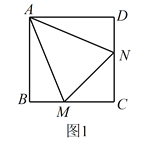
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .(不必证明)
.(不必证明)
(1)当![]() 绕点
绕点![]() 旋转到
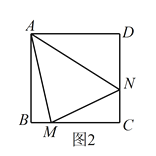
旋转到![]() 时(如图2),线段
时(如图2),线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明。
之间有怎样的数量关系?写出猜想,并加以证明。
(2)当![]() 绕点
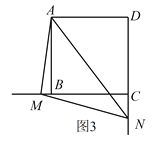
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() ,
,![]() 和
和![]() 之间又有怎样的数量关系?写出猜想,并加以证明。
之间又有怎样的数量关系?写出猜想,并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径为6,则GE+FH的最大值为( )
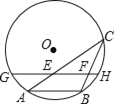
A. 6 B. 9 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com