
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() ,
,![]() (或它们的延长线)于点
(或它们的延长线)于点![]() ,
,![]() 。当
。当![]() 绕点
绕点![]() 旋转到
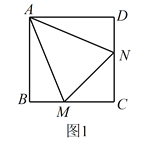
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .(不必证明)
.(不必证明)
(1)当![]() 绕点
绕点![]() 旋转到
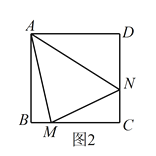
旋转到![]() 时(如图2),线段
时(如图2),线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明。
之间有怎样的数量关系?写出猜想,并加以证明。
(2)当![]() 绕点
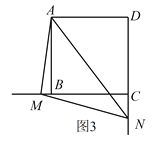
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() ,
,![]() 和
和![]() 之间又有怎样的数量关系?写出猜想,并加以证明。
之间又有怎样的数量关系?写出猜想,并加以证明。
【答案】(1)BM+DN=MN;(2)BM+DN=MN;(3)DN﹣BM=MN.
【解析】
(1)连接AC,交MN于点G,则可知AC垂直平分MN,结合∠MAN=45°,可证明△ABM≌△AGM,可得到BM=MG,同理可得到NG=DN,可得出结论;
(2)在MB的延长线上,截取BE=DN,连接AE,则可证明△ABE≌△ADN,可得到AE=AN,进一步可证明△AEM≌△ANM,可得结论BM+DN=MN;
(3)在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,进一步可证明△MAN≌△FAN,可得到MN=NF,从而可得到DN﹣BM=MN
(1)如图1,连接AC,交MN于点G.
∵四边形ABCD为正方形,∴BC=CD,且BM=DN,∴CM=CN,且AC平分∠BCD,∴AC⊥MN,且MG=GN,∴∠MAG=∠NAG.
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,∴∠BAM=∠GAN=∠GAM.在△ABM和△AGM中,∵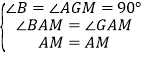 ,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN,∴BM+DN=MN;
,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN,∴BM+DN=MN;
(2)猜想:BM+DN=MN.证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE.在△ABE和△ADN中,∵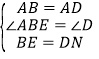 ,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,∵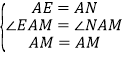 ,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
(3)DN﹣BM=MN.证明如下:
如图3,在DC上截取DF=BM,连接AF,△ABM和△ADF中,∵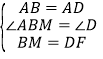 ,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即MAF=∠BAD=90°.
,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即MAF=∠BAD=90°.
∵∠MAN=45°,∴∠MAN=∠FAN=45°.
在△MAN和△FAN中,∵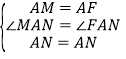 ,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.
,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,点E是边AD上动点,点F是边BC上动点,连接EF,把矩形ABCD沿直线EF折叠,点B恰好落在边AD上,记为点G;如图2,把矩形展开铺平,连接BE,FG.

(1)判断四边形BEGF的形状一定是 ,请证明你的结论;
(2)若矩形边AB=4,BC=8,直接写出四边形BEGF面积的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形![]() 在平面直角坐标系中的位置如图所示,
在平面直角坐标系中的位置如图所示,![]() ,
,![]() ,AC=4,把平行四边形
,AC=4,把平行四边形![]() 绕点
绕点![]() 逆时针方向旋转,使点
逆时针方向旋转,使点![]() 落在
落在![]() 轴上,则旋转后点
轴上,则旋转后点![]() 的对应点
的对应点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)直接写出OC=___________;
(2)如图1,当CP与⊙A相切时,求PO的长;
(3)如图2,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问当PO为何值时,△OCQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,在边长为![]() 个单位长度的小正方形组成的方格中,点
个单位长度的小正方形组成的方格中,点![]() 都在格点上.
都在格点上.
(1)画出ΔABC绕着点B逆时针旋转90°得到的ΔA'B'C',并写出的A'的坐标__________
(2)在(1)的情况下,直接写出线段AA’的长度____________.
(3)在y轴上找一点P,使ΔPAB的周长最小,直接写出P的坐标_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣![]() 与 是关于1的平衡数;
与 是关于1的平衡数;
(2)若(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,判断m+
,判断m+![]() 与5﹣
与5﹣![]() 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,设一次函数![]() 的图象是直线
的图象是直线![]() .
.
(1)如果把![]() 向下平移
向下平移![]() 个单位后得到直线
个单位后得到直线![]() ,求
,求![]() 的值;
的值;
(2)当直线![]() 过点
过点![]() 和点
和点![]() 时,且
时,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若坐标平面内有点![]() ,不论
,不论![]() 取何值,点
取何值,点![]() 均不在直线
均不在直线![]() 上,求
上,求![]() 所需满足的条件.
所需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com