
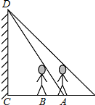
【题目】墙壁![]() 处有一盏灯(如图),小明站在
处有一盏灯(如图),小明站在![]() 处测得他的影长与身长相等都为
处测得他的影长与身长相等都为![]() ,小明向墙壁走
,小明向墙壁走![]() 到
到![]() 处发现影子刚好落在A
处发现影子刚好落在A![]() 点,则灯泡与地面的距离
点,则灯泡与地面的距离![]() ________.
________.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知线段a,P为线段a上任意一点,已知图形M,Q为图形M上任意一点,当P,Q两点间的距离最小时,将此时PQ的长度称为图形M与线段a的近点距;当P,Q两点间的距离最大时,将此时PQ的长度称为图形M与线段a的远点距.

根据阅读材料解决下列问题:
如图1,在平面直角坐标系xOy中,点A的坐标为(﹣2,﹣2),正方形ABCD的对称中心为原点O.
(1)线段AB与线段CD的近点距是 ,远点距是 .
(2)如图2,直线y=﹣x+6与x轴,y轴分别交于点E,F,则线段EF和正方形ABCD的近点距是 ,远点距是 ;
(3)直线y=x+b(b≠0)与x轴,y轴分别交于点R,S,线段RS与正方形ABCD的近距点是![]() ,则b的值是 ;
,则b的值是 ;
(4)在平面直角坐标系xOy中,有一个矩形GHMN,若此矩形至少有一个顶点在以O为圆心1为半径的圆上,其余各点可能在圆上或圆内,将正方形ABCD绕点O旋转一周,在旋转过程中,它与矩形GHMN的近点距的最小值是 ,远点距的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
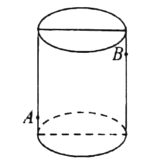
【题目】有一个圆柱形玻璃杯高![]() ,底面周长为
,底面周长为![]() ,有一只蚂蚁在一侧距下底
,有一只蚂蚁在一侧距下底![]() 的外侧
的外侧![]() 点,与点
点,与点![]() 正对的容器内侧距下底
正对的容器内侧距下底![]() 的
的![]() 点处有一饭粒,蚂蚁想吃
点处有一饭粒,蚂蚁想吃![]() 处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________
处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() ,
,![]() (或它们的延长线)于点
(或它们的延长线)于点![]() ,
,![]() 。当
。当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .(不必证明)
.(不必证明)
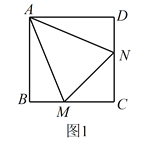
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明。
之间有怎样的数量关系?写出猜想,并加以证明。
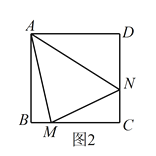
(2)当![]() 绕点
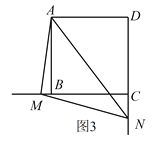
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() ,
,![]() 和
和![]() 之间又有怎样的数量关系?写出猜想,并加以证明。
之间又有怎样的数量关系?写出猜想,并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上一点,
上一点,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
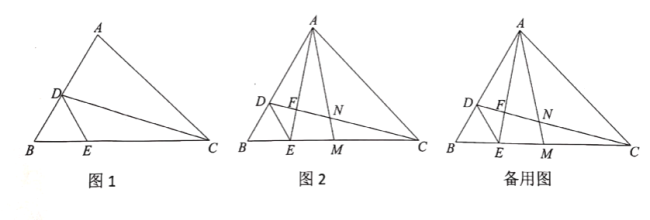
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,直接写出线段
,直接写出线段![]() ,
,![]() ,
,![]() 的等量关系.
的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F.
(1)求证:△CBE≌△CDF;
(2)若AB=3,DF=2,求AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com