【题目】平行四边形
在平面直角坐标系中的位置如图所示，
，
，AC=4，把平行四边形绕点
逆时针方向旋转，使点
落在
轴上，则旋转后点
的对应点
的坐标为________．
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，过B作一直线与CD相交于点E，过A作AF垂直BE于点F，过C作CG垂直BE于点G，在FA上截取FH=FB，再过H作HP垂直AF交AB于P．若CG=3．则△CGE与四边形BFHP的面积之和为 _________ ．
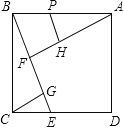
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为梦之点，例如，点（1，1），（﹣ 2，﹣ 2），（
，），…，都是梦之点，显然梦之点有无数个．
（1）若点 P（2，b）是反比例函数
(n 为常数，n ≠ 0) 的图象上的梦之点，求这个反比例函数解析式；
（2）⊙O 的半径是 ，
①求出⊙O上的所有梦之点的坐标；
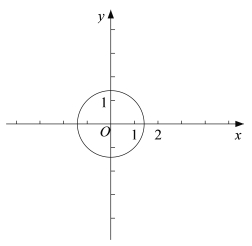
②已知点 M（m，3），点 Q 是（1）中反比例函数 图象上异于点 P 的梦之点，过点Q 的直线 l 与 y 轴交于点 A，∠OAQ＝45°．若在⊙ O 上存在一点 N，使得直线 MN ∥ l或 MN ⊥ l，求出 m 的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表是三种电话计费方式：
月使用费 （元） | 主叫限定时间 （分钟） | 主叫超时收费 （元/分钟） | 被叫 | |
方式一 | 18 | 60 | 0.2 | 免费 |
方式二 | 28 | 120 | 0.2 | 免费 |
方式三 | 48 | 240 | 0.2 | 免费 |
说明：月使用费固定收取，主叫不超限定时间不再收费，主叫超时部分加收超时费.
设一个月内主叫通话
分钟（为正整数）.
（1）当
时，按方式一计费为______元；按方式二计费为______元.
（2）当
时，是否存在某一时间，使方式二与方式三的计费结果相等？若存在，请求出对应的值，若不存在，请说明理由.
（3）当
时，哪一种收费方式最省钱？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一个圆柱形玻璃杯高
，底面周长为
，有一只蚂蚁在一侧距下底
的外侧
点，与点正对的容器内侧距下底
的
点处有一饭粒，蚂蚁想吃处的饭粒，要从杯子的外侧爬到杯子的内侧，杯子的厚度忽略不计，则至少需要爬________________
。
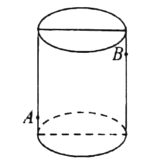
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年10月某服装店老板用15000元购得“衬衣”和“T恤”共200件，其中“衬衣”和“T恤”的数量比为3：2，已知每件“衬衣”的售价比每件“T恤”的售价的2倍少20元，预计10月可全部售完．
（1）该批发商想通过本次销售共获利1800元，则每件“衬衣”卖多少元？
（2）实际销售时，受中央“厉行节约”号召的影响，在（1）中销售价的基础之上，“衬衣”的销售量不变，售价下降了a%，“T恤”的销售量下降了2a%，但售价不变，结果“衬衣”比“T恤”的销售额至少多了6480元，求a的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
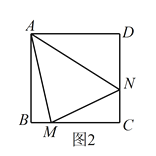
【题目】已知：正方形
中，
，
绕点
顺时针旋转，它的两边分别交
，
（或它们的延长线）于点
，
。当绕点旋转到
时（如图1），易证
．（不必证明）
（1）当绕点旋转到
时（如图2），线段
，
和
之间有怎样的数量关系？写出猜想，并加以证明。
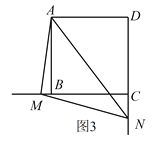
（2）当绕点旋转到如图3的位置时，线段，和之间又有怎样的数量关系？写出猜想，并加以证明。
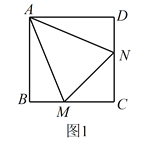
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，已知直线y=-2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．
（1）求点A、C的坐标；
（2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；
（3）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
