
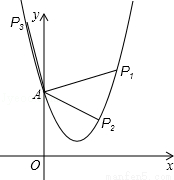
菱形与正方形的形状有差异,我们将菱形与正方形的接近程度记为“接近度”.设菱形相邻的两个内角的度数分别为m°和n°,将菱形与正方形的“接近度”定义为|m-n|.在平面直角坐标系中,抛物线y=x2+ bx+c(b<0)交y轴于点A(与原点O不同),以AO为边作菱形OAPQ.
bx+c(b<0)交y轴于点A(与原点O不同),以AO为边作菱形OAPQ.
(1)当c=- b时,抛物线上是否存在点P,使菱形OAPQ与正方形的“接近度”为0,请说明理由.
b时,抛物线上是否存在点P,使菱形OAPQ与正方形的“接近度”为0,请说明理由.
(2)当c>0时,对于任意的b,抛物线y=x2+ bx+c上是否存在点P,满足菱形OAPQ与正方形的“接近度”为60?若存在,请求出所有满足条件的b与c的关系式;若不存在,请说明理由.
bx+c上是否存在点P,满足菱形OAPQ与正方形的“接近度”为60?若存在,请求出所有满足条件的b与c的关系式;若不存在,请说明理由.
(1)理由见解析;(2)b=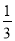 -
-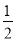 c.
c.
【解析】
试题分析:(1)表示出点A的坐标,再根据正方形的四条边都相等且每一个角都是直角取点P的坐标,然后根据二次函数图象上点的坐标特征进行验证即可;
(2)根据“接近度”的定义求出m、n的值,然后分点P在y轴右侧时,∠OAP=120°和∠OAP=60°两种情况求出点P的坐标,再代入抛物线解析式求出b、c的关系式,然后根据b<0求出c的取值范围,进行验证即可;点P在y轴左侧时,只有∠OAP=120°,表示出点P的坐标,再代入抛物线解析式得到b、c的关系式,然后根据b<0求出c的取值范围,再进行验证.
试题解析:(1)存在.
当c=-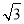 b时,点A的坐标为(0,-
b时,点A的坐标为(0,-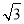 b),
b),
取P(-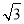 b,-
b,-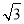 b),
b),
当x=-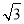 b时,y=(-
b时,y=(-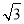 b)2+
b)2+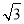 b×(-
b×(-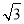 b)-
b)-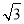 b=-
b=-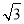 b,
b,
故点P在抛物线上,且OA=AP,OA⊥P,
∴m=n=90,
∴抛物线上存在点P,使菱形OAPQ与正方形的“接近度”为0;
(2)【解析】
∵菱形OAPQ与正方形的“接近度”为60,
∴|m-n|=60,
又∵m+n=180,
∴m=120,n=60或m=60,n=120,
当P在y轴右侧时:①当∠OAP=120°时,P1(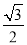 c,
c,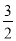 c)且在y=x2+
c)且在y=x2+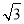 bx+c上,
bx+c上,
∴(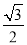 c)2+
c)2+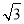 b×
b×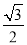 c+c=
c+c=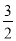 c,
c,
∴b=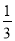 -
-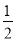 c,
c,
∵b<0,
∴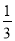 -
-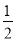 c<0,
c<0,
解得c>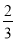 ,
,
即当c>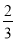 时,b与c的关系式为b=
时,b与c的关系式为b=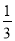 -
-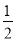 c;
c;
②当∠OAP=60°时,P2(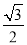 c,
c,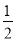 c),且在y=x2+
c),且在y=x2+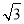 bx+c上,
bx+c上,
∴(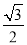 c)2+
c)2+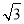 b×
b×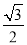 c+c=
c+c=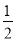 c,
c,
∴b=-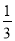 -
-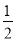 c,
c,
∵b<0,
∴-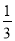 -
-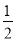 c<0,
c<0,
解得c>-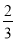 ,
,
举例:当b=-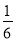 时,c=-
时,c=-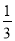 <0,不满足对任意b,c>0,不符合题意;
<0,不满足对任意b,c>0,不符合题意;
当P在y轴左侧时:只可能存在∠OAP=120°,P3(-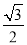 c,
c,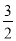 c)且在y=x2+
c)且在y=x2+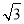 bx+c上,
bx+c上,
∴(-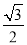 c)2+
c)2+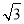 b×(-
b×(-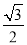 c)+c=
c)+c=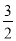 c,
c,
∴b=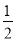 c-
c-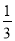 ,
,
∵b<0,
∴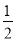 c-
c-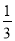 <0,
<0,
解得c<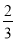 ,
,
举例:当b=-1时,c=-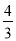 ,不满足对任意b,c>0,不符合题意;
,不满足对任意b,c>0,不符合题意;
综上所述,b与c的关系式为b=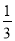 -
-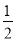 c.
c.
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年辽宁省盘锦市中考第一次模拟考试数学试卷(解析版) 题型:填空题
2014年3月8日马航失踪后,党中央、国务院高度重视,3月12日前,我国已划定长90海里,宽25海里,总面积约2250平方海里(约合7717平方公里)的长方形区域为的海上搜救范围,1平方公里=1×106平方米,对7717平方公里用科学计数法表示为__________ 平方米。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:解答题
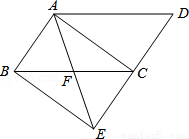
如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)连接AC、BE,则当∠AFC与∠D满足什么条件时,四边形ABEC是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:填空题
已知反比例函数y= (x>0),请你补充一个条件 ,使y的值随着x值的增大而减小.
(x>0),请你补充一个条件 ,使y的值随着x值的增大而减小.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:选择题
正方形网格中,∠AOB如图放置,则sin∠AOB=( )

A.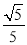 B.
B.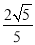 C.
C.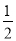 D.2
D.2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:解答题
如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:填空题
2013年12月2日凌晨,中国“嫦娥三号”探月器飞天成功.飞行了5天左右,进入与地球相距384000千米的月球轨道.数384000用科学计数法表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com