
【题目】如图,在四边形ABCD中,AC⊥CD于点C,BD平分∠ADC交AC于点E,∠1=∠2.
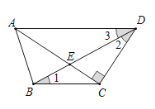
(1) 请完成下面的说理过程.
∵BD平分∠ADC(已知)
∴ (角平分线的定义)
∵∠1=∠2(已知)
∴
∴AD∥BC( )
(2)若∠BCE=20°,求∠1的度数.
【答案】(1)∠2=∠3,∠1=∠3,内错角相等,两直线平行;(2)35°
【解析】
(1)根据角平分线的定义,及平行线的判定定理即可求证;
(2)根据平行线的性质定理,可得∠ADC+∠BCD=180°,求得∠ADC度数,由(1)得∠1=∠2=∠3,即可求得∠1度数.
(1)∵BD平分∠ADC(已知)
∴∠2=∠3(角平分线的定义)
∵∠1=∠2(已知)
∴∠1=∠3
∴AD∥BC(内错角相等,两直线平行)
故答案为:∠2=∠3,∠1=∠3,内错角相等,两直线平行
(2)∵AC⊥CD
∴∠ACD=90°
∵∠BCE=20°
∴∠BCD=20°+90°=110°
∵AD∥BC
∴∠ADC+∠BCD=180°
∴∠ADC=180°-110°=70°
∵∠1=∠2=∠3=35°
故答案为:35°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦)长为37.4m,拱高(弧的中点到弦的距离)为7.2m,请求出赵州桥的主桥拱半径(结果保留小数点后一位).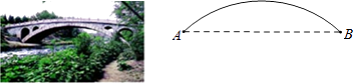
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法①△ABC中,若∠A+∠B=90°,则△ABC是直角三角形;②已知正n边形的一个内角为140,则这个正多边形的边数是9;③一个多边形的内角中最多有3个锐角;④三角形的外角一定大于内角;⑤若不等式组![]() 的整数解恰好有2个,则m的取值范围是
的整数解恰好有2个,则m的取值范围是![]() ,其中说法正确的是_____________________(填写说法正确的序号)
,其中说法正确的是_____________________(填写说法正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则△AFC的面积等于___.
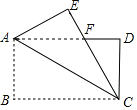
【答案】![]()
【解析】
由矩形的性质可得AB=CD=4,BC=AD=6,AD//BC,由平行线的性质和折叠的性质可得∠DAC=∠ACE,可得AF=CF,由勾股定理可求AF的长,即可求△AFC的面积.
解:![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 折叠
折叠
![]() ,
,
![]()
![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
![]() .
.
故答案为:![]() .
.
【点睛】
本题考查了翻折变换,矩形的性质,勾股定理,利用勾股定理求AF的长是本题的关键.
【题型】填空题
【结束】
12
【题目】某公司要招聘一名新的大学生,公司对入围的甲、乙两名候选人进行了三项测试,成绩如表所示,根据实际需要,规定能力、技能、学业三项测试得分按5:3:2的比例确定个人的测试成绩,得分最高者被录取,此时______将被录取.
得分 | 能力 | 技能 | 学业 |
甲 | 95 | 84 | 61 |
乙 | 87 | 80 | 77 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=∠C,点D在BC上,点E在AC上,连接DE且∠ADE=∠AED
(1)若∠B=70°,∠ADE=80°,求∠BAD,∠CDE.
(2)当点D在BC(点B,C除外)边上运动时,且点E在AC边上,猜想∠BAD与∠CDE的数量关系是,并证明你的猜想.

(3)当点D在BC(点B,C除外)边上运动时,且点E在AC边上,若∠BAD=25°,求∠CDE.

查看答案和解析>>
科目:初中数学 来源: 题型:
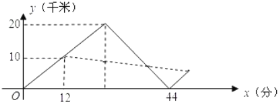
【题目】2018年5月,某城遭遇暴雨水灾,武警战士乘一冲锋舟从A地逆流而上,前往C地营救受困群众,途经B地时,由所携带的救生艇将B地受困群众运回A地,冲锋舟继续前进,到C地接到群众后立刻返回A地,途中曾与救生艇相遇,冲锋舟和救生艇距A地的距离y(千米)和冲锋舟出发后所用时间x(分)之间的函数图象如图所示,假设群众上下冲锋舟和救生艇的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(1)冲锋舟从A地到C地的时间为 分钟,冲锋舟在静水中的速度为 千米/分,水流的速度为 千米/分.
(2)冲锋舟将C地群众安全送到A地后,又立即去接应救生艇,已知救生艇与A地的距离y(千米)和冲锋舟出发后所用时间x(分钟)之间的函数关系式为y=kx+b,若冲锋舟在距离A地![]() 千米处与救生艇第二次相遇,求k、b的值.
千米处与救生艇第二次相遇,求k、b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com