练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．如图，将边长为1的正方形OAPB沿x轴正方向连续翻转2016次，点P依次落在点P1，P2，P3，P4，…，P2016的位置，则P2016的坐标为（2015，1）．

    分析 可按题意分别求出P1，P2，P6…的横坐标，再总结出规律即可得出P2016的坐标．

    解答 解：根据规律
    P1（1，1），P2（2，0）=P3，P4（3，1），
    P5（5，1）P6（6，0）=P7，P8（7，1）…，
    每4个一循环，可以判断P2016在504次循环后与P4一致，坐标应该是（2015，1），
    故答案是：（2015，1）．

    点评 本题考查了点的坐标的规律性，根据规律得出P2016在504次循环后与P4一致是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．解方程组：$\left\{\begin{array}{l}{3x+4y=15}\\{2x-4y=10}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，将一个边长为1的正方形纸片分割成6部分，部分①是整体面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依此类推．
    （1）图中阴影部分的面积是$\frac{1}{32}$；
    （2）写出$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n+1}}$的结果；
    （3）计算$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{6}}$+$\frac{1}{{2}^{7}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算
    （1）（-12）-5+（-14）-（-39）
    （2）-12016+|-6|×$\frac{1}{2}$+（-$\frac{1}{2}$）3×（-2）4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．三边长均为整数且周长为24的三角形的个数为（　　）
    A．11B．12C．17D．18

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

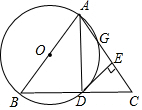    13．如图，以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D，交AC于点G，连结AD，并过点D作⊙O的切线DE，交AC于点E．求证：
    （1）BD=CD；
    （2）DE⊥AC；
    （3）CE=EG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

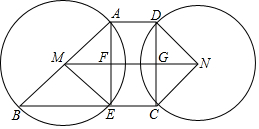    20．如图，已知四边形BCNM是平行四边形，分别以M，N为圆心，以MB，NC为半径作圆，⊙M交BC于E，AB为⊙M的直径，连接AE交MN于F，过C点作MN的垂线MN于G，交⊙N于D，连接DN．
    （1）求证：四边形ADCE是矩形；
    （2）已知：AB：MN=5：7
    ①若tanB=0.75，求证：四边形ADCE是正方形；
    ②若四边形ADCE是正方形，那么tanB一定等于0.75吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知G为△ABC的重心，过G的直线交AB于P，交AC于Q，设$\frac{AP}{PB}$=a，$\frac{AQ}{QC}$=b，则$\frac{1}{a}$+$\frac{1}{b}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

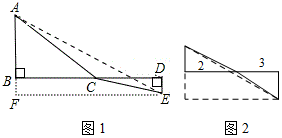    18．如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=5，DE=1，BD=8，设CE=x
    （1）请求出AC+CE的最小值．
    （2）请构图求出代数式$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-24x+153}$的最小值．

    查看答案和解析>>

    同步练习册答案