
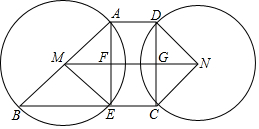
 如图,已知四边形BCNM是平行四边形,分别以M,N为圆心,以MB,NC为半径作圆,⊙M交BC于E,AB为⊙M的直径,连接AE交MN于F,过C点作MN的垂线MN于G,交⊙N于D,连接DN.
如图,已知四边形BCNM是平行四边形,分别以M,N为圆心,以MB,NC为半径作圆,⊙M交BC于E,AB为⊙M的直径,连接AE交MN于F,过C点作MN的垂线MN于G,交⊙N于D,连接DN.分析 (1)首先证明四边形ECGF是矩形,再证明四边形AFGD是矩形,即可解决问题.
(2)①由AB:MN=5:7,可以假设AB=5k,MN=7k,则NM=BC=7k,在Rt△ABE中,tan∠ABE=$\frac{AE}{BE}$=$\frac{3}{4}$,设AE=3x,BE=4x,可得(3x)2+(4x)2=(5k)2,推出x=k,推出AE=3k,BE=4k,推出EC=BC-BE=7k-4k=3k,推出AE=EC,由此即可解决问题.
②不一定.因为四边形AECD是正方形,设AE=EC=a,在Rt△ABE中,由AB2=AE2+BE2,可得(5k)2=a2+(7k-a)2,推出a=3k或a=4k,当a=3k时,AE=3k,BE=4k,tan∠ABE=$\frac{AE}{BE}$=$\frac{3}{4}$=0.75,当a=4k时,AE=4k,BE=3k,tan∠ABE=$\frac{AE}{BE}$=$\frac{4}{3}$,由此即可判断.
解答 证明:(1)∵AB是直径,
∴∠AEB=90°,
∵四边形BCNM是平行四边形,
∴MN∥BC,
∴∠AFM=∠AEB=90°,
∴MF⊥AE,
∴AF=EF,
∵CD⊥MN,
∴∠CGF=∠GFE=∠FEC=90°,
∴四边形ECGF是矩形,
∴AE∥DC,EF=CG=AF,
∵NG⊥CD,
∴DG=CG=AF,
∴四边形AFGD是平行四边形,
∵∠AFG=90°,
∴四边形AFGD是矩形,
∴∠EAD=∠ADC=∠AEC=90°,
∴四边形AECD是矩形.
(2)①∵AB:MN=5:7,
∴可以假设AB=5k,MN=7k,则NM=BC=7k,
在Rt△ABE中,tan∠ABE=$\frac{AE}{BE}$=$\frac{3}{4}$,设AE=3x,BE=4x,
∴(3x)2+(4x)2=(5k)2,
∴x=k,
∴AE=3k,BE=4k,
∴EC=BC-BE=7k-4k=3k,
∴AE=EC,
∵四边形AECD是矩形,
∴四边形AECD是正方形.
②不一定.理由如下,
∵AB:MN=5:7,
∴可以假设AB=5k,MN=7k,则NM=BC=7k,
∵四边形AECD是正方形,设AE=EC=a,
在Rt△ABE中,∵AB2=AE2+BE2,
∴(5k)2=a2+(7k-a)2,
整理得a2-7ka+12k2=0,
∴(a-3k)(a-4k)=0,
∴a=3k或a=4k,
当a=3k时,AE=3k,BE=4k,tan∠ABE=$\frac{AE}{BE}$=$\frac{3}{4}$=0.75,
当a=4k时,AE=4k,BE=3k,tan∠ABE=$\frac{AE}{BE}$=$\frac{4}{3}$,
∴tanB的值不一定等于0.75.
点评 本题考查圆综合题、平行四边形的性质、矩形的判定和性质、正方形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会利用参数,构建方程解决问题,体现了数形结合的数学思想,属于中考压轴题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:填空题
 如图,点P是∠AOB的角平分线OC上任意一点,D、E点分别在射线OA、OB上,要使△POD≌△POE,还需添加一个条件,这个条件可以是OD=OE(写一种即可).
如图,点P是∠AOB的角平分线OC上任意一点,D、E点分别在射线OA、OB上,要使△POD≌△POE,还需添加一个条件,这个条件可以是OD=OE(写一种即可).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2016次,点P依次落在点P1,P2,P3,P4,…,P2016的位置,则P2016的坐标为(2015,1).
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2016次,点P依次落在点P1,P2,P3,P4,…,P2016的位置,则P2016的坐标为(2015,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{(-3)}^2}}$=-3 | B. | a2+a4=a6 | C. | ${({-\frac{1}{2}})^{-1}}$=2 | D. | (-π)0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | D. | $\frac{\sqrt{18}-\sqrt{8}}{2}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
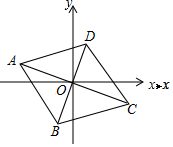 如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )| A. | (4,-2) | B. | (4,2) | C. | (2,-4) | D. | (-2,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com