
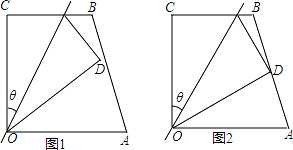
如图 1,四边形 OABC 中,OA=a,OC=8,∠AOC=∠BCO=90°,经过点 O 的直线 l 将四边形分 成两部分,直线 l 与 OC 所成的角设为 θ,将四边形 OABC 的直角∠OCB 沿直线 l 折叠,点 C 落在 点 D 处(如图 1).
(1)若点 D 与点 A 重合,则 θ= ,a= ; 若折叠后点 D 恰为 AB 的中点(如图 2),求 θ 的度数.
【考点】翻折变换(折叠问题).
【分析】(1)利用轴对称的性质即可解决问题;
延长 MD、OA,交于点 N,如图 2.易证△BDM≌△ADN,则有 DM=DN,根据垂直平分线的性质 可得 OM=ON,根据等腰三角形的性质可得∠MOD=∠NOD,从而就可求出 θ.
【解答】解:(1)若点 D 与点 A 重合, 则 θ=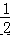 ∠COA=45°,OA=OC=8.
∠COA=45°,OA=OC=8.
故答案为:45°,8.
如图:延长 MD、OA,交于点 N.
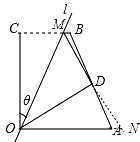
∵∠AOC=∠BCO=90°,
∴∠AOC+∠BCO=180°,
∴BC∥OA,
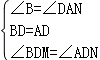 ∴∠B=∠DAN. 在△BDM 和△AD
∴∠B=∠DAN. 在△BDM 和△AD N 中,
N 中,
,
∴△BDM≌△ADN(ASA),
∴DM=DN.
∵∠ODM=∠OCM=90°,
∴根据线段垂直平分线的性质可得 OM=ON,
∴根据等腰三角形的性质可得∠MOD=∠NOD. 由折叠可得∠MOD=∠MOC=θ,
∴∠COA=3θ=90°,
∴θ=30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有 ,
, ,那么下列说法中错误的是( ).
,那么下列说法中错误的是( ).
A.红花、绿花种植面积一定相等 B.紫花、橙花种植面积一定相等
C.红花、蓝花种植面积一定相等 D.蓝花、黄花种植面积一定相等

查看答案和解析>>
科目:初中数学 来源: 题型:
以四边形 的边
的边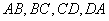 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为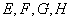 ,顺次连结这四个点,得四边形
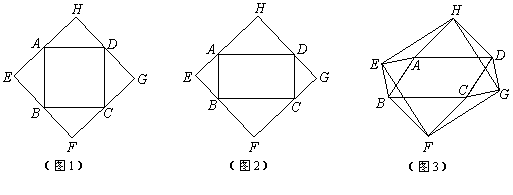
,顺次连结这四个点,得四边形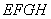 .如图1,当四边形
.如图1,当四边形 为正方形时,我们发现四边形
为正方形时,我们发现四边形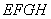 是正方形.
是正方形.
(1)如图2,当四边形 为矩形时,请判断:四边形
为矩形时,请判断:四边形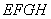 的形状(不要求证明);
的形状(不要求证明);
(2)如图3,当四边形 为一般平行四边形时,若
为一般平行四边形时,若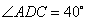 ,
,
①试求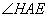 的度数;
的度数;
②求证: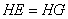 ;
;
③请判定四边形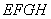 是什么四边形?并说明理由.
是什么四边形?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com