
如图,在 Rt△ABC 和 Rt△BCD 中,∠A=∠D=90°,AB=CD=4,BC=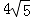 ,△BCE 的面积= .
,△BCE 的面积= .
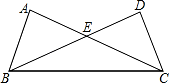
10【考点】全等三角形的判定与性质.
【分析】根据全等三角形的判定求出△ABE≌△DCE,根据全等三角形的性质得出 BE=CE,在 Rt△ABC 中,由勾股定理求出 AC,在 Rt△ABE 中,由勾股定理求出 BE,根据三角形面积公式求 出即可.
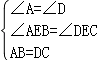 【解答】解:在△ABE 和△DCE 中,
【解答】解:在△ABE 和△DCE 中,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,
在 Rt△ABC 中,∠A=90°,AB=4,BC=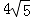 ,由勾股定理得:AC=
,由勾股定理得:AC= 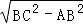 =8, 在 Rt△ABE 中,由勾股定理得:AB2+AE2=BE2,
=8, 在 Rt△ABE 中,由勾股定理得:AB2+AE2=BE2,
42+(8﹣BE)2=BE2,
解得:BE=5,
∴△BCE 的面积 S=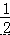 ×BE×DC=
×BE×DC= 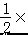 5×4=10.
5×4=10.
故答案为:10.
【点评】本题考查了全等三角形的性质和判定,勾股定理的应用,能求出 BE=CE 是解此题的关键.


科目:初中数学 来源: 题型:
已知从山脚起每升高 100 米,气温就下降 0.6 摄氏度,现测得山脚处的气温为 14.1 摄氏度,山上 点 P 处的气温为 11.1 摄氏度,则点 P 距离山脚处的高度为( )
A.50 米B.200 米 C.500 米 D.600 米
查看答案和解析>>
科目:初中数学 来源: 题型:
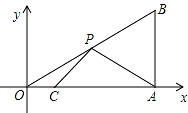
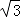 如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
画图:试画出下列正多边形的所有对称轴,并完成表格,
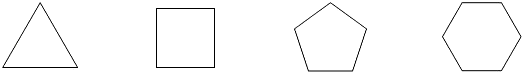
| 正多边形的边数 | 3 | 4 | 5 | 6 | 7 | … |
| 对称轴的条数 | … |
 根据上表,猜想正 n 边形有 n 条对称轴.
根据上表,猜想正 n 边形有 n 条对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
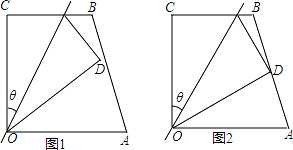
如图 1,四边形 OABC 中,OA=a,OC=8,∠AOC=∠BCO=90°,经过点 O 的直线 l 将四边形分 成两部分,直线 l 与 OC 所成的角设为 θ,将四边形 OABC 的直角∠OCB 沿直线 l 折叠,点 C 落在 点 D 处(如图 1).
(1)若点 D 与点 A 重合,则 θ= ,a= ; 若折叠后点 D 恰为 AB 的中点(如图 2),求 θ 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com