
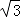 如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
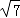 +2【考点】轴对称-最短路线问题;坐标与图形性质.
+2【考点】轴对称-最短路线问题;坐标与图形性质.
【分析】作 A 关于 OB 的对称点 D,连接 CD 交 OB 于 P,连接 AP,过 D 作 DN⊥OA 于 N,则此 时 PA+PC 的值最小,求出 AM,求出 AD,求出 DN、CN,根据勾股定理求出 CD,即可得出答案.
【解答】解:作 A 关于 OB 的对称点 D,连接 CD 交 OB 于 P,连接 AP,过 D 作 DN⊥OA 于 N, 则此时 PA+PC 的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
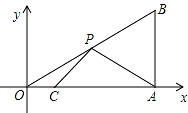
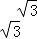 ∵B(3, ),
∵B(3, ),
∴AB= ,OA=3,∠B=60°,由勾股定理得:OB=2 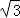 , 由三角形面积公式得:
, 由三角形面积公式得: 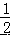 ×OA×AB=
×OA×AB= 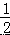 ×OB×AM,
×OB×AM,
∴AM= 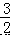 ,
,
∴AD=2× 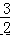 =3,
=3,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN= 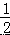 AD=
AD= 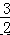 ,由勾股定理得:DN=
,由勾股定理得:DN= 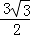 ,
,
∵C(1,0),
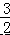
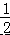 ∴CN=AC﹣AN=2﹣ = ,
∴CN=AC﹣AN=2﹣ = ,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
一次函数 y=x+5 的图象经过点 P(a,b)和 Q(c,d),则 a(c﹣d)﹣b(c﹣d)的值为( )
A.9 B.﹣16 C.25 D.﹣25
查看答案和解析>>
科目:初中数学 来源: 题型:
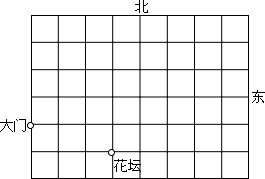
这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).
(1)根据上述条件建立平面直角坐标系;
建筑物 A 的坐标为(3,1),请在图中标出 A 点的位置.
(3)建筑物 B 在大门北偏东 45°的方向,并且 B 在花坛的正北方向处,请直接写出 B 点的坐标.
(4)在 y 轴上找一点 C,使△ABC 是以 AB 腰的等腰三角形,请直接写出点 C 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
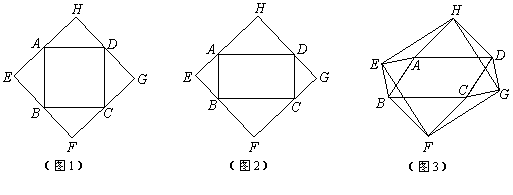
以四边形 的边
的边 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为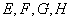 ,顺次连结这四个点,得四边形
,顺次连结这四个点,得四边形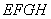 .如图1,当四边形
.如图1,当四边形 为正方形时,我们发现四边形
为正方形时,我们发现四边形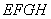 是正方形.
是正方形.
(1)如图2,当四边形 为矩形时,请判断:四边形
为矩形时,请判断:四边形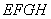 的形状(不要求证明);
的形状(不要求证明);
(2)如图3,当四边形 为一般平行四边形时,若
为一般平行四边形时,若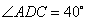 ,
,
①试求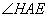 的度数;
的度数;
②求证: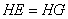 ;
;
③请判定四边形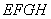 是什么四边形?并说明理由.
是什么四边形?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com