
以四边形 的边
的边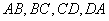 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为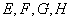 ,顺次连结这四个点,得四边形
,顺次连结这四个点,得四边形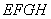 .如图1,当四边形
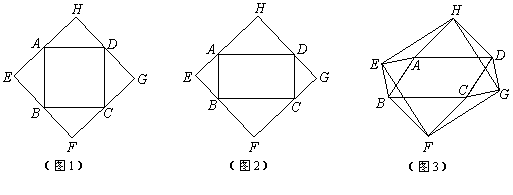
.如图1,当四边形 为正方形时,我们发现四边形
为正方形时,我们发现四边形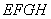 是正方形.
是正方形.
(1)如图2,当四边形 为矩形时,请判断:四边形
为矩形时,请判断:四边形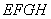 的形状(不要求证明);
的形状(不要求证明);
(2)如图3,当四边形 为一般平行四边形时,若
为一般平行四边形时,若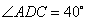 ,
,
①试求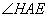 的度数;
的度数;
②求证: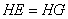 ;
;
③请判定四边形 是什么四边形?并说明理由.
是什么四边形?并说明理由.

(1)四边形EFGH是正方形.…………2分
(2) ①∵∠ADC=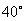 ,
,
在□ABCD中,AB∥CD,∴∠BAD=180°-∠ADC=140°;
∵△HAD和△EAB都是等腰直角三角形,∴∠HAD=∠EAB=45°,
∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-140°=130°.………4分
②∵△AEB和△DGC都是等腰直角三角形,∴△AEB≌△CGD,∴AE=BE=CG=DG,
在□ABCD中,AB=CD,∴AE=DG,∵△HAD和△GDC都是等腰直角三角形,
∴∠DHA=∠CDG= 45°,∴∠HDG=∠HAE.
∵△HAD是等腰直角三角形,∴HA=HD,∴△HAE≌△HDG,∴HE=HG.…………6分
③四边形EFGH是正方形.
由②同理可得:GH=GF,FG=FE,∵HE=HG(已证),∴GH=GF=FG=FE,
∴四边形EFGH是菱形;∵△HAE≌△HDG(已证),∴∠DHG=∠AHE,
又∵∠AHD=∠AHG+∠DHG=90°,∴∠EHG=∠AHG+∠AHE=90°,
∴四边形EFGH是正方形.………………9分


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
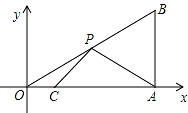
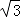 如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
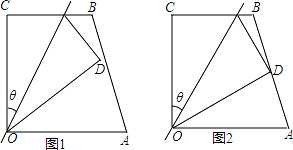
如图 1,四边形 OABC 中,OA=a,OC=8,∠AOC=∠BCO=90°,经过点 O 的直线 l 将四边形分 成两部分,直线 l 与 OC 所成的角设为 θ,将四边形 OABC 的直角∠OCB 沿直线 l 折叠,点 C 落在 点 D 处(如图 1).
(1)若点 D 与点 A 重合,则 θ= ,a= ; 若折叠后点 D 恰为 AB 的中点(如图 2),求 θ 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
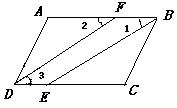 已知:如图,
已知:如图,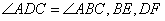 分别
分别
平分 且
且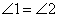 .
.
求证: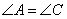 .
.
证明:∵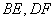 分别平分
分别平分 ( 已知 ),
( 已知 ),
∴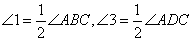 ( ),
( ),
∵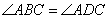 ( 已知 ).
( 已知 ).
∴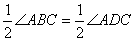 ( ),
( ),
∴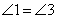 ( ),
( ),
又因为∵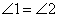 ( ),
( ),
∴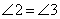 ( ).
( ).
∴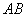 ∥
∥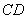 ( ),
( ),
∴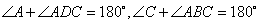 ( ).
( ).
∴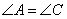 ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣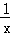 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2 C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,线段AB的长为1。C1为AB的中点;C2为C1B的中点;…Cn为Cn-1B的中点(n是正整数)。观察思考:AC1= ,换个角度有AC1=AB-C1B=1
,换个角度有AC1=AB-C1B=1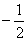 ;AC2=
;AC2=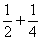 ,换个角度有AC2=AB-C2B=1
,换个角度有AC2=AB-C2B=1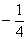 ;…ACn=
;…ACn=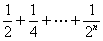 ,换个角度有AC=AB-CnB=____。(用含n的代数式表示)由此我们得到
,换个角度有AC=AB-CnB=____。(用含n的代数式表示)由此我们得到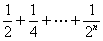 的计算方法。
的计算方法。
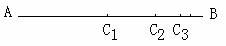 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com