
【题目】如图,抛物线y=ax2+c经过点A(0,2)和点B(-1,0).
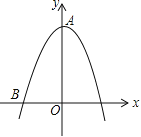
(1)求此抛物线的解析式;
(2)将此抛物线平移,使其顶点坐标为(2,1),平移后的抛物线与x轴的两个交点分别为点C,D(点C在点D的左边),求点C,D的坐标;
(3)将此抛物线平移,设其顶点的纵坐标为m,平移后的抛物线与x轴两个交点之间的距离为n,若1<m<3,直接写出n的取值范围.
【答案】(1)y=-2x2+2;(2)C( 2-![]() ,0),D(2+
,0),D(2+![]() ,0)(3)
,0)(3)![]() <n<
<n<![]() .
.
【解析】
试题(1)把点A、B的坐标分别代入函数解析式,列出关于a、c的方程组,通过解方程求得它们的值;
(2)根据平移的规律写出平移后抛物线的解析式,然后令y=0,则解关于x的方程,即可求得点C、D的横坐标;
(3)根据根与系数的关系来求n的取值范围;
试题解析:(1)∵抛物线y=ax2+c经过点A(0,2)和点B(-1,0).
∴![]()
解得:![]()
∴ 此抛物线的解析式为y=-2x2+2;
(2)∵ 此抛物线平移后顶点坐标为(2,1),
∴ 抛物线的解析式为y=-2(x-2)2+1
令y=0,即-2(x-2)2+1=0
解得 x1=2+![]() ,x2=2-
,x2=2-![]() .
.
∵ 点C在点D的左边
∴ C( 2-![]() ,0),D(2+
,0),D(2+![]() ,0)
,0)
(3)![]() <n<
<n<![]() .
.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
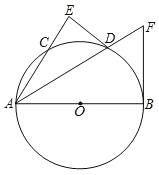
【题目】如图,AB是直经,D是![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
(1)求证:DE是⊙O的切线.
(2)试探究AE,AD,AB三者之间的等量关系.
(3)若DE=3,⊙O的半径为5,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3AB=3![]() ,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=______.
,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
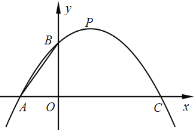
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
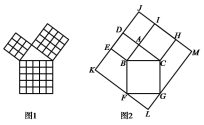
【题目】在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,![]() ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
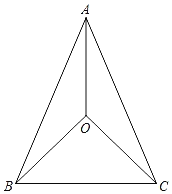
【题目】如图,在△ABC中,AB=AC,点O为∠BAC的平分线上一点,连接OB、OC.
(1)求证:OB=OC;
(2)若OA=OC,∠BAC=46°,求∠OCB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=![]() ,若CE
,若CE![]() DE=5,则正方形的面积为( )
DE=5,则正方形的面积为( )
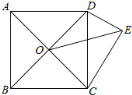
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
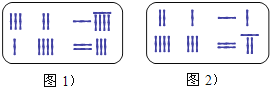
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com