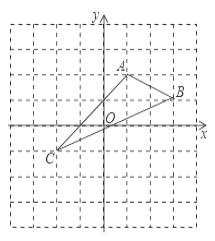
[题目]如图.在平面直角坐标系中.A(1.2).B(3.1).C(-2.-1)．(1)在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标,(2)求出△A1B1C1的面积．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平面直角坐标系中，A(1，2)，B(3，1)，C(－2，－1)．

（1）在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标；

（2）求出△A1B1C1的面积．

【答案】（1）图见解析；点A1的坐标为（﹣1,2），点B1的坐标为（﹣3,1），点C1的坐标为（2, ﹣1）；（2）.

【解析】

（1）先根据轴对称的性质作出△A1B1C1，然后再写出各点坐标即可；

（2）用一个长方形将△A1B1C1框住，再利用长方形的面积减去三个直角三角形的面积即可.

解：（1）如图所示：△A1B1C1即为所求.由图可知：点A1的坐标为（﹣1,2），点B1的坐标为（﹣3,1），点C1的坐标为（2, ﹣1）.

（2）用一个长方形将△A1B1C1框住，如上图所示：

由图可知：△A1B1C1的面积=5×3－×1×2－×2×5－×3×3=

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB＝AC，E在线段AC上，D在线段AB的延长线上，连DE交BC于F，过点E作EG⊥BC于G，若BD＝CE，求证：FG＝BF＋CG．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】一玩具城以元/个的价格购进某种玩具进行销售，并预计当售价为元/个时，每天能售出个玩具，且在一定范围内，当每个玩具的售价平均每提高元时，每天就会少售出个玩具

若玩具售价不超过元/个，每天售出玩具总成本不高于元，预计每个玩具售价的取值范围；

在实际销售中，玩具城以中每个玩具的最低售价及相应的销量为基础，进一步调整了销售方案，将每个玩具的售价提高了，从而每天的销售量降低了，当每天的销售利润为元时，求的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．

(1)求证：△ACE≌△BCD；

(2)若AD＝5，BD＝12，求DE的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中，点A（2，0），B（0，4），若以B，O，C为顶点的三角形与△ABO全等，则点C的坐标不能为（　　）

A.（0，﹣4）B.（﹣2，0）C.（2，4）D.（﹣2，4）

查看答案和解析>>

科目：初中数学 来源： 题型：

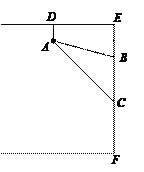
【题目】下图是投影仪安装截面图．教室高EF＝3.5 m，投影仪A发出的光线夹角∠BAC＝30°，投影屏幕高BC＝1.2 m．固定投影仪的吊臂AD＝0.5 m，且AD⊥DE，AD∥EF，∠ACB＝45°．求屏幕下边沿离地面的高度CF（结果精确到0.1 m）．

（参考数据：tan15°≈0.27，tan30°≈0.58）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】李航想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，李航边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得李航落在墙上的影子高度CD=1.2m，CE=0.6m，CA=30m（点A、E、C在同一直线上）．已知李航的身高EF是1.6m，请你帮李航求出楼高AB．