
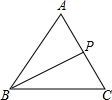
 如图,在边长为1的正三角形ABC中,P是AC边上的一个动点,(不与两端重合),设PC=x,△ABP的面积为S
如图,在边长为1的正三角形ABC中,P是AC边上的一个动点,(不与两端重合),设PC=x,△ABP的面积为S分析 (1)先求出AC边长的高线,然后根据三角形的面积公式可求得S与x的函数关系式;
(2)将x的值代入求得S的值即可.
解答 解:(1)过点B作BD⊥AC,垂足为D.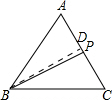
∵△ABC为正三角形,BD⊥AC,
∴∠ABD=$\frac{1}{2}∠ABC$=30°.
∴BD=AB•cos30°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
∵PC=x,AC=1,
∴AP=1-x.
∴S=$\frac{1}{2}AP•BD$=$\frac{1}{2}×\frac{\sqrt{3}}{2}(1-x)$=-$\frac{\sqrt{3}}{4}x+\frac{\sqrt{3}}{4}$.
∴S与x的函数关系式为:S=-$\frac{\sqrt{3}}{4}x+\frac{\sqrt{3}}{4}$.
(2)当x=0.2时,S=-$\frac{\sqrt{3}}{4}×\frac{1}{5}+\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{5}$;
当x=0.5时,S=-$\frac{\sqrt{3}}{4}×\frac{1}{2}+\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{8}$.
点评 本题主要考查的是求函数的关系式,求得AC边上的高线的长度是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com