Question

10．如图，△ABC内接于⊙O，AD平分∠BAC交⊙O于D，连接OD交BC于H．

（1）求证：OD⊥BC；
（2）若OH=DH，求∠BAC的度数；
（3）若AB=6，AC=4，过B作BK⊥AD于K，连接HK，求HK的长．

Answer 1

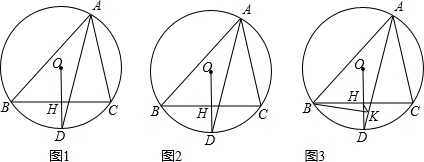
分析 （1）如图1，证明$\widehat{BD}$=$\widehat{CD}$，运用垂径定理及其推论，即可解决问题．
（2）如图2，首先求出∠BOH的度数，运用圆周角定理即可解决问题．
（3）如图3，作辅助线，首先证明△BAK≌△MAK，得到BK=MK，进而判断HK为△BCM的中位线，即可解决问题．

解答 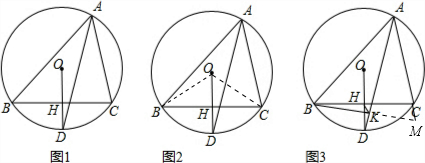（1）证明：如图1，
∵AD平分∠BAC，
∴$\widehat{BD}$=$\widehat{CD}$，
∴OD⊥BC；
（2）如图2，连接OB、OC；
∵OH=DH，OB=OD，
∴OH=$\frac{1}{2}$OB，而OH⊥BH，
∴∠OBH=30°，∠BOH=60°
∴∠BAC=$\frac{1}{2}$∠BOC=60°．
（3）如图3，分别延长BK、AC，交于点M；
∵AD平分∠BAC，
∴∠BAK=∠MAK；
在△BAK与△MAK中，
$\left\{\begin{array}{l}{AB=AM}\\{∠BAK=∠MAK}\\{AK=AK}\end{array}\right.$，
∴△BAK≌△MAK（SAS），
∴BK=MK，AM=AB=6；
∵OD⊥BC，
∴BH=HC，
∴HK为△BCM的中位线，
∴HK=$\frac{1}{2}$CM=$\frac{1}{2}$（6-4）=1．

点评 此题考查了圆周角定理、垂径定理、全等三角形的判定等知识．该题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．