
【题目】如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )

A. ③④ B. ①② C. ①②③ D. ②③④
【答案】C
【解析】
由△ABC中,∠ABC与∠ACB的平分线交于点F,DE∥BC,易证得△BDF和△CEF都是等腰三角形,继而可得DE=BD+CE,又由△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;即可得△ADE的周长等于AB与AC的和.
∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵△ABC中,∠ABC与∠ACB的平分线交于点F,
∴∠DBF=∠FBC,∠ECF=∠FCB,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
即△BDF和△CEF都是等腰三角形;
故①正确;
∴DE=DF+EF=BD+CE,
故②正确;
∴△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;
故③正确;
∵∠ABC不一定等于∠ACB,
∴∠FBC不一定等于∠FCB,
∴BF与CF不一定相等,
∴BD与CE不一定相等,故④错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图. 
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图。 
(1)问题 如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证: ![]() .
.
(2)探究 如图,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用 请利用(1)(2)获得的经验解决问题
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以D为圆心,DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数. 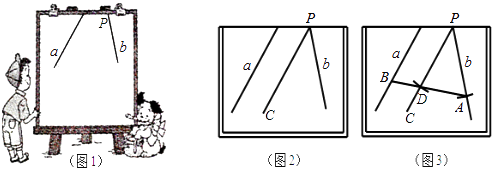
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1 ,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为________.
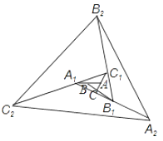
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com