
【题目】如图所示双曲线y=![]() 与
与![]() 分别位于第三象限和第二象限,A是y轴上任意一点,B是
分别位于第三象限和第二象限,A是y轴上任意一点,B是![]() 上的点,C是y=
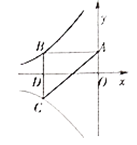
上的点,C是y=![]() 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为-3,则C点的坐标为(-3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为-3,则C点的坐标为(-3, ![]() );③k=4;④△ABC的面积为定值7.正确的有( )
);③k=4;④△ABC的面积为定值7.正确的有( )
A. I个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】(1)由图可知,反比例函数![]() 的一个分支位于第三象限,
的一个分支位于第三象限,
∴双曲线![]() 在每个象限内,y随x的增大而减小,即说法①正确;
在每个象限内,y随x的增大而减小,即说法①正确;
(2)若B的横坐标为-3,则点B的坐标为(-3,1),
∴此时BD=1,
∵4BD=3CD,
∴3CD=4,
∴CD=![]() ,
,
∵点C在第三象限,
∴点C的坐标为![]() ,即说法②错误;
,即说法②错误;
(3)设点B的坐标为![]() ,则BD=
,则BD=![]() ,
,
∵4BD=3CD,
∴3CD=![]() ,
,
又∵点C在第三象限,BC⊥x轴,
∴此时,点C的坐标为![]() ,
,
∵点C在反比例函数![]() 的图象上,
的图象上,
∴![]() ,即说法③正确;
,即说法③正确;
(4)设点B的坐标为![]() ,则由(3)可知,此时点C的坐标为
,则由(3)可知,此时点C的坐标为![]() ,
,
∴BC=![]() ,
,
∵点A是y轴上一点,
∴点A到BC的距离为![]() ,
,
∴S△ABC=![]() AC·(
AC·(![]() )=
)=![]() ,即说法④错误.
,即说法④错误.
综上所述,正确的说法是①③,共2个.
故选B.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
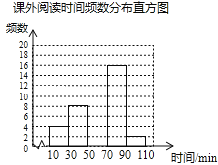
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
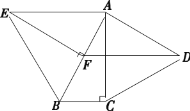
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
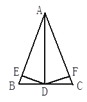
【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论: (1) DE=DF; (2) AD上任一点到点C、点B的距离相等; (3) BD=CD,AD⊥BC;(4)∠BDE=∠CDF,其中,正确的有__________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线ykx3经过点B(-![]() ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 ![]() 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠OAB 的度数;
(2)抛物线![]() 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.
(3)在抛物线![]() 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
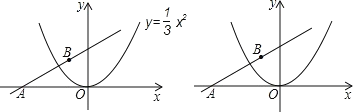
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF分别与AB、CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°.
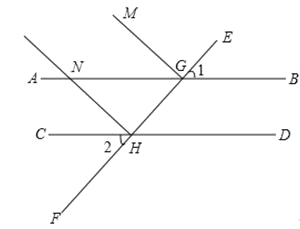
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N分别以点M、N为圆心,以大于![]() MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=
MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=![]() ∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
∠ABC;③BC=BE;④AE=BE中,一定正确的是( )

A. ①②③B. ① ② ④C. ①③④D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com