
【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
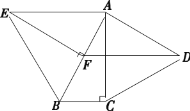
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
【答案】(1)见详解;(2)见详解.
【解析】
(1)由△ABE是等边三角形可知:AB=BE,∠EBF=60°,于是可得到∠EFB=∠ACB=90°,∠EBF=∠ABC,接下来依据AAS证明△ABC≌△EBF即可;
(2)由△ABC≌△EBF可得到EF=AC,由△ACD是的等边三角形进而可证明AC=AD=EF,然后再证明∠BAD=90°,可证明EF∥AD,故此可得到四边形EFDA为平行四边形.
解:(1)证明:∵△ABE是等边三角形,EF⊥AB,
∴∠EBF=60°,AE=BE,∠EFB=90°.
又∵∠ACB=90°,∠ABC=60°,
∴∠EFB=∠ACB,∠EBF=∠ABC.
∵BE=BA,
∴△ABC≌△EBF(AAS).
(2)证明:∵△ABC≌△EBF,
∴EF=AC.
∵△ACD是的等边三角形,
∴AC=AD=EF,∠CAD=60°,
又∵Rt△ABC中,∠ABC=60°,∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=90°,
∴∠EFA=∠BAD=90°,
∴EF∥AD.
又∵EF=AD,
∴四边形EFDA是平行四边形.


科目:初中数学 来源: 题型:
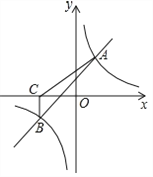
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() <
<![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
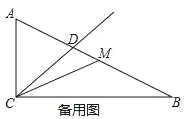
【题目】如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.
(1)求线段CD的长;
(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;
(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数y=![]() ,y=
,y=![]() 在第一象限内的图象如图所示,点P1,P2,P3,....,P99,在反比例函数y=
在第一象限内的图象如图所示,点P1,P2,P3,....,P99,在反比例函数y=![]() 图象上,它们的横坐标分别是x1,x2,x3,....,x99,纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1,P2,P3,…,P99分别作y轴的平行线线,与y=
图象上,它们的横坐标分别是x1,x2,x3,....,x99,纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1,P2,P3,…,P99分别作y轴的平行线线,与y=![]() 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),.....,Q99(x99,y99),则y99=______
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),.....,Q99(x99,y99),则y99=______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,BE与CF交于点D,则对于下列结论:
,BE与CF交于点D,则对于下列结论:![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() 在
在![]() 的平分线上
的平分线上![]() 其中正确的是( )
其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
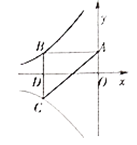
【题目】如图所示双曲线y=![]() 与
与![]() 分别位于第三象限和第二象限,A是y轴上任意一点,B是
分别位于第三象限和第二象限,A是y轴上任意一点,B是![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为-3,则C点的坐标为(-3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为-3,则C点的坐标为(-3, ![]() );③k=4;④△ABC的面积为定值7.正确的有( )
);③k=4;④△ABC的面积为定值7.正确的有( )
A. I个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中, ABC 90, CD AD , BE AD , AD2 CD2 2 AB2,若四边形 ABCD 的面积为18,则 BE 的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com