
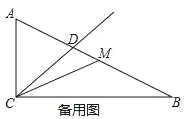
【题目】如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.
(1)求线段CD的长;
(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;
(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)CP的长是
;(3)CP的长是![]() 或
或![]() 或
或![]() .
.
【解析】分析:(1)作辅助线,证明四边形ECFD是正方形,设DF=x,则CF=x,BF=2﹣x,由△BDF∽△BAC,得![]() ,可得CD的长;
,可得CD的长;
(2)如图2,作辅助线,构建全等三角形,先根据C、B、P、A四点共圆,得∠APB=90°,可知AP=BP,由角平分线性质得:PM=PN,根据HL证明Rt△PMA≌Rt△PNB(HL),得AM=BN,设AM=x,则PM=CM=x+1,CN=2﹣x,由CM=CN列方程可得x的值,可得CD的长;
(3)存在三种情况:
①当PM=CM时,如图3,同理作出辅助线,根据△PCM是等腰直角三角形,可得CP的长;
②先根据勾股定理求AB=![]() ,根据直角三角形斜边中线等于斜边一半可得CP的长;
,根据直角三角形斜边中线等于斜边一半可得CP的长;
③由△CPN∽△CMH,列比例式结合①可得CP的长.
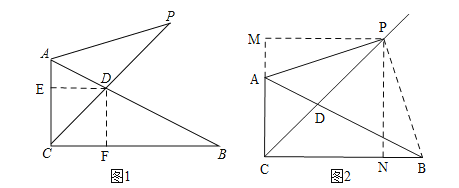
详解:(1)如图1,过D作DE⊥AC于E,DF⊥BC于F.
∵DF平分∠ACB,∠ACB=90°,∴DE=DF.
∵∠DEC=∠ACB=∠CFD=90°,
∴四边形ECFD是正方形.
设DF=x,则CF=x,BF=2﹣x.
∵DF∥AC,∴△BDF∽△BAC,
∴![]() ,∴x=
,∴x=![]() .
.
∵△CDE是等腰直角三角形,∴CD=![]() ;
;
(2)如图2.∵∠PAB=∠PCB=45°,
∴C、B、P、A四点共圆,∴∠ACB+∠APB=180°.
∵∠ACB=90°,∴∠APB=90°,
∴△APB是等腰直角三角形,∴AP=BP.
过P作PM⊥AC于M,PN⊥BC于N,连接PB.
∵PM=PN,∴R△PMA≌Rt△PNB(HL),∴AM=BN.
由(1)知:四边形MCNP是正方形,∴CM=CN.
设AM=x,则PM=CM=x+1,CN=2﹣x,
∴x+1=2﹣x,x=![]() ,∴CM=
,∴CM=![]() ,∴CP=
,∴CP=![]() ;
;
(3)若△CMP是等腰三角形,存在三种情况:
①当PM=CM时,如图3,同理作出辅助线.
∵∠PCN=45°,∴△PCM是等腰直角三角形,∴CN=PN,
同(2)得:CP=![]() ;
;
②Rt△ACB中,AC=1,BC=2,∴AB=![]() .
.
∵M是AB的中点,∴CM=CP=![]() AB=
AB=![]() ;
;
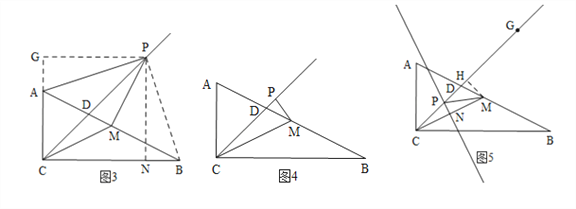
③作CM的中垂线交CD于P,则CP=PM,过M作MH⊥CD于H.
由①知:CG(就是CP=![]() )=
)=![]() ,CH=
,CH=![]() .
.
∵△CPN∽△CMH,∴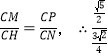 =
=![]() ,CP=
,CP=![]() .
.
综上所述:CP的长是![]() 或
或![]() 或
或![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】我省教育厅下发了![]() 在全省中小学幼儿园广泛开展节约教育的通知
在全省中小学幼儿园广泛开展节约教育的通知![]() ,通知中要求各学校全面持续开展“光盘行动”
,通知中要求各学校全面持续开展“光盘行动”![]() 深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度
深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度![]() 程度分为:“A:了解很多”、“B:了解较多”、“C:了解较少”、“D:不了解”
程度分为:“A:了解很多”、“B:了解较多”、“C:了解较少”、“D:不了解”![]() ,对本市某所中学的学生进行了抽样调查
,对本市某所中学的学生进行了抽样调查![]() 我们将这次调查的结果绘制了以下两幅不完整统计图:
我们将这次调查的结果绘制了以下两幅不完整统计图:
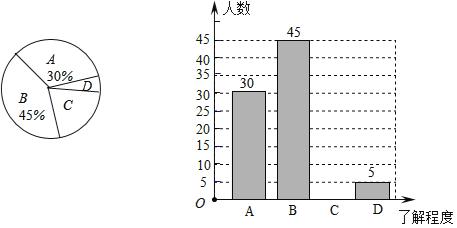
根据以上信息,解答下列问题:
![]() 补全条形统计图;
补全条形统计图;
![]() 本次抽样调查了______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
本次抽样调查了______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
![]() 若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?
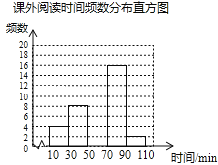
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
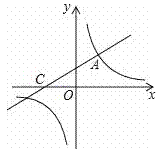
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列两个条件下,分别求代数式![]() 和
和![]() 的值,将结果直接填写在下面的横线上:
的值,将结果直接填写在下面的横线上:
①当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
②当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)观察结果,你有什么发现?请写出结论,并再任选a、b的值加以验证;
(3)利用你的发现,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
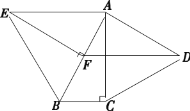
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF分别与AB、CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°.
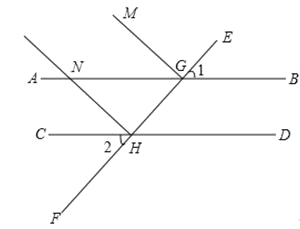
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com