
【题目】在钝角三角形ABC中,把AB=AC,D是BC上一点,AD把![]() ABC分成两个等腰三角形,则
ABC分成两个等腰三角形,则![]() BAC的度数为( )
BAC的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据等腰三角形的性质可得∠B=∠BAD,∠ADC=∠DAC,∠B=∠C,再由三角形外角的性质可得∠ADC=∠B+∠BAD=2∠B,设∠B=x°,则∠DAC=∠ADC=2x°,∠BAC=3x°,由三角形的内角和定理可得x+x+3x=180,解方程求得x的值,即可求得![]() BAC的度数.
BAC的度数.
如图,
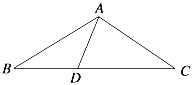
根据题意,△ABD、△ADC是等腰三角形,
∴∠B=∠BAD,∠ADC=∠DAC,
∵AB=AC,
∴∠B=∠C,
根据三角形外角的性质可得,
∠ADC=∠B+∠BAD=2∠B,
设∠B=x°,则∠DAC=∠ADC=2x°,∠BAC=3x°,
根据三角形内角和,x+x+3x=180,
解得x=36,
∴∠BAC=3x°=108°.
故选D.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】(1)在下列两个条件下,分别求代数式![]() 和
和![]() 的值,将结果直接填写在下面的横线上:
的值,将结果直接填写在下面的横线上:
①当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
②当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)观察结果,你有什么发现?请写出结论,并再任选a、b的值加以验证;
(3)利用你的发现,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD,等边△ ABE.已知∠ABC=60°,EF⊥AB,垂足为 F,连接 DF.
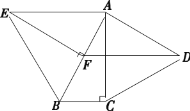
(1)证明:△ACB≌△EFB;
(2)求证:四边形 ADFE 是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年 7 月 1 日,《上海市生活垃圾管理条例》正式实施,生活垃圾按照“可回收物”、 “有害垃圾”、“湿垃圾”、“干垃圾”的分类标准.没有垃圾分类和未指定投放到指定垃圾桶内等会被罚款和行政处罚.垃圾分类制度即将在全国范围内实施,很多商家推出售卖垃圾分类桶,某商店经销垃圾分类桶.现有如下信息:
信息 1:一个垃圾分类桶的售价比进价高 12 元;
信息 2:卖 3 个垃圾分类桶的费用可进货该垃圾分类桶 4 个;
请根据以上信息,解答下列问题:
(1)该商品的进价和售价各多少元?
(2)商店平均每天卖出垃圾分类桶 16 个.经调查发现,若销售单价每降低 1 元,每天可多售出 2 个.为了使每天获取更大的利润,垃圾分类桶的售价为多少元时,商店每天获取的利润最大?每天的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论: (1) DE=DF; (2) AD上任一点到点C、点B的距离相等; (3) BD=CD,AD⊥BC;(4)∠BDE=∠CDF,其中,正确的有__________个.
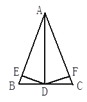
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线ykx3经过点B(-![]() ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 ![]() 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠OAB 的度数;
(2)抛物线![]() 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.
(3)在抛物线![]() 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
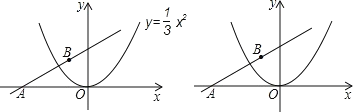
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF分别与AB、CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°.
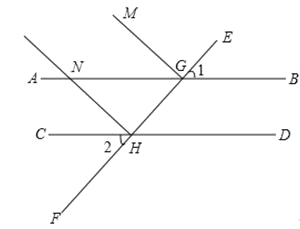
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中,对角线 BD 的垂直平分线 MN 与 AD 相交于点 M ,与 BD 相交于点 N ,连接 BM 、 DN .
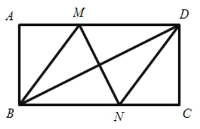
(1)求证: BN DM ;
(2)若 AB 4 , AD 8,求 MD 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com