
分析 (1)设某数为x,则某数与1的差可表示为x-1,这个数的2倍可表示为2x,然后建立等量关系;再把x=4代入方程左右两边,根据一元一次方程的解的定义判断4是否为方程的解.
(2)设某数为x,某数与2的差的$\frac{1}{2}$可表示为$\frac{1}{2}$(x-2),该数的2倍与4的差的$\frac{1}{2}$可表示为$\frac{1}{2}$(2x-4),然后利用两者的数量关系列方程;再把x=4代入方程左右两边,根据一元一次方程的解的定义判断4是否为方程的解.
解答 解:(1)设某数为x,
根据题意得x-1=2x.
当x=4时,x-1=3,2x=8,所以x=4不是方程x-1=2x的解;
(2)设某数为x,
根据题意得$\frac{1}{2}$(x-2)=$\frac{1}{2}$(2x-4)-1.
当x=4时,$\frac{1}{2}$(x-2)=1,$\frac{1}{2}$(2x-4)-1=1,所以x=4是方程$\frac{1}{2}$(x-2)=$\frac{1}{2}$(2x-4)-1的解.
点评 本题考查了由实际问题抽象出一元一次方程:审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.也考查了一元一次方程的解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
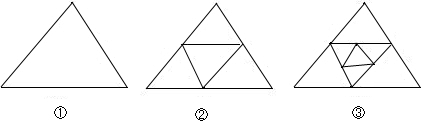
| 图形编号 | ① | ② | ③ | ④ | ⑤ | … |
| 三角形个数 | 1 | 5 | 9 | 13 | 17 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com