
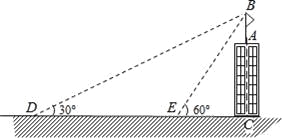
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )
A. 调查全体女生 B. 调查全体男生
C. 调查九年级全体学生 D. 调查七,八,九年级各100名学生
查看答案和解析>>
科目:初中数学 来源: 题型:
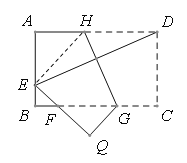
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.有抛物线![]() 和
和![]() .抛物线
.抛物线![]() 经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线
经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线![]() 上一点,且在x轴上方.过点P作x轴的垂线交抛物线
上一点,且在x轴上方.过点P作x轴的垂线交抛物线![]() 于点Q.过点Q作PQ的垂线交抛物线
于点Q.过点Q作PQ的垂线交抛物线![]() 于点
于点![]() (不与点Q重合),连结
(不与点Q重合),连结![]() .设点P的横坐标为m.
.设点P的横坐标为m.

(1)求a的值;
(2)当抛物线![]() 经过原点时,设△
经过原点时,设△![]() 与△OAB重叠部分图形的周长为l.
与△OAB重叠部分图形的周长为l.
①求![]() 的值;
的值;
②求l与m之间的函数关系式;
(3)当h为何值时,存在点P,使以点O、A、Q、![]() 为顶点的四边形是轴对称图形?直接写出h的值.
为顶点的四边形是轴对称图形?直接写出h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
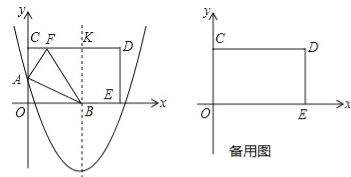
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com