
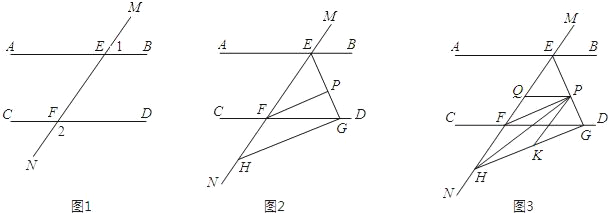
����Ŀ����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������
��1�����ж�ֱ��AB��ֱ��CD��λ�ù�ϵ����˵�����ɣ�
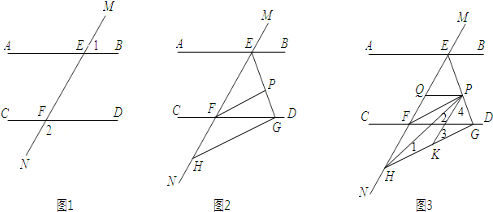
��2����ͼ2����BEF���EFD�Ľ�ƽ���߽��ڵ�P��EP��CD���ڵ�G����H��MN��һ�㣬��GH��EG����֤��PF��GH��
��3����ͼ3���ڣ�2���������£�����PH��K��GH��һ��ʹ��PHK����HPK����PQƽ�֡�EPK���ʡ�HPQ�Ĵ�С�Ƿ����仯�������䣬�������ֵ�����仯��˵�����ɣ�
���𰸡���1��֤������������2��֤������������3��45��
��������
���⣨1�����öԶ�����ȡ���������������֪ͬ���ڽǡ�AEF����CFE������������֤AB��CD��
��2�����ã�1����ƽ���ߵ�������֪�㣻Ȼ����ݽ�ƽ���ߵ����ʡ��������ڽǺͶ���֤�á�EPF=90�㣬��EG��PF���ʽ����֪����GH��EG����֤PF��GH��
��3��������������Ƕ������������ڽǺͶ�����á�4=90��-��3=90��-2��2��Ȼ�����ڲ��ǵĶ��塢��ƽ���ߵĶ�����֪��QPK=![]() ��EPK=45��+��2��������ͼ���еĽ���Ǽ�ĺͲ��ϵ��á�HPQ�Ĵ�С���䣬�Ƕ�ֵ45�㣮
��EPK=45��+��2��������ͼ���еĽ���Ǽ�ĺͲ��ϵ��á�HPQ�Ĵ�С���䣬�Ƕ�ֵ45�㣮
�����������1����ͼ1��
�ߡ�1���2������
���1+��2=180�㣮
�֡ߡ�1=��AEF����2=��CFE��
���AEF+��CFE=180�㣬
��AB��CD��
��2����ͼ2���ɣ�1��֪��AB��CD��
���BEF+��EFD=180�㣮
�֡ߡ�BEF���EFD�Ľ�ƽ���߽��ڵ�P��
���FEP+��EFP=![]() ����BEF+��EFD��=90�㣬
����BEF+��EFD��=90�㣬
���EPF=90�㣬��EG��PF��
��GH��EG��
��PF��GH��
��3����HPQ�Ĵ�С�������仯���������£�
��ͼ3���ߡ�1=��2��
���3=2��2��
�֡�GH��EG��
���4=90��-��3=90��-2��2��
���EPK=180��-��4=90��+2��2��
��PQƽ�֡�EPK��
���QPK=![]() ��EPK=45��+��2��
��EPK=45��+��2��
���HPQ=��QPK-��2=45�㣬
���HPQ�Ĵ�С�������仯��һֱ��45�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() ��
�� ![]() ��ֱ����
��ֱ���� ![]() ���ң�
���ң� ![]() ��
�� ![]() ����������
���������� ![]() ��ͼ����Ӱ���֣�Χ��һ��Բ�IJ��棬�����Բ����Բ�İ뾶�� ��
��ͼ����Ӱ���֣�Χ��һ��Բ�IJ��棬�����Բ����Բ�İ뾶�� �� 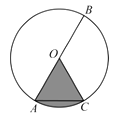
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У������²�����ͼ������AΪԲ�ģ����ⳤΪ�뾶�������ֱ�AB��AD�ڵ�M��N���ڷֱ���M��NΪԲ�ģ��Դ��� ![]() MN�ij�Ϊ�뾶�����������ཻ�ڵ�P������AP���ߣ�����CD�ڵ�Q����DQ=2QC��BC=3����ƽ���ı���ABCD�ܳ�Ϊ ��
MN�ij�Ϊ�뾶�����������ཻ�ڵ�P������AP���ߣ�����CD�ڵ�Q����DQ=2QC��BC=3����ƽ���ı���ABCD�ܳ�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����DBE�У�BC=BE������Ҫ����������������ʹ��ABC�ա�DBE���������ӵ�һ�������ǣ� ��
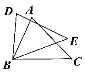
A. AC=DE����C=��E B. BD=AB��AC=DE C. AB=DB����A=��D D. ��C=��E����A=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪����������y= ![]() x��ͼ���뷴��������y=
x��ͼ���뷴��������y= ![]() ��ͼ����A��a����2����B���㣮
��ͼ����A��a����2����B���㣮 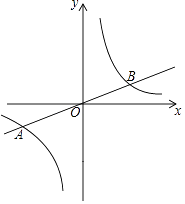
��1�����������ı���ʽ�͵�B�����ꣻ
��2��P�ǵ�һ�����ڷ���������ͼ����һ�㣬����P��y���ƽ���ߣ���ֱ��AB�ڵ�C������PO������POC�����Ϊ3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��y�ᣬ����ΪB������ABO�Ƶ�A��ʱ����ת����AB1O1��λ�ã�ʹ��B�Ķ�Ӧ��B1����ֱ��y=�� ![]() x�ϣ��ٽ���AB1O1�Ƶ�B1��ʱ����ת����A1B1O1��λ�ã�ʹ��O1�Ķ�Ӧ��O2����ֱ��y=��
x�ϣ��ٽ���AB1O1�Ƶ�B1��ʱ����ת����A1B1O1��λ�ã�ʹ��O1�Ķ�Ӧ��O2����ֱ��y=�� ![]() x�ϣ����ν�����ȥ������B�������ǣ�0��1�������O12��������Ϊ ��
x�ϣ����ν�����ȥ������B�������ǣ�0��1�������O12��������Ϊ �� 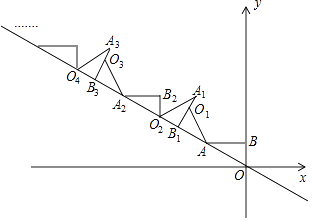
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����˳ɳ���Ӱ���Ǿ�ģ�һ�����������ܸı��˵�һ������ͼ��ijУ�����꼶ѧ�������ֲ�������ͳ��ͼ�����а��꼶ѧ������Ϊ408�ˣ��±��Ǹ�Уѧ���Ķ������鼮���ͳ�Ʊ�������ͼ���е���Ϣ����֪��Уѧ��ƽ��ÿ�˶�������ı�����(����)
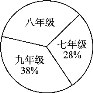
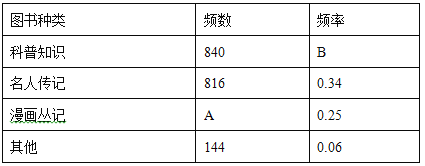
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�ı�OA��OC�ֱ���x�ᡢy���ϣ���B�ڵ�һ���ޣ���D�ڱ�BC�ϣ��ҡ�AOD=30�㣬�ı���OA��B��D���ı���OABD����ֱ��OD�Գƣ���A���A��B���B�ֱ��Ӧ������AB=1������������y= ![]() ��k��0����ͼ��ǡ�þ�����A�䣬B����k��ֵΪ ��
��k��0����ͼ��ǡ�þ�����A�䣬B����k��ֵΪ �� 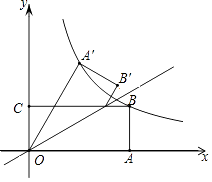
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com