
【题目】数学课上老师设计了一个数学游戏:若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”。甲、乙、丙、丁四位同学各有一张多项式卡片,下面是甲、乙、丙、丁四位同学的对话:
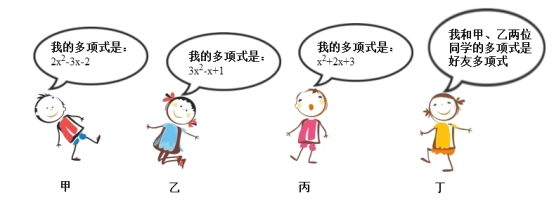
请根据对话解答下列问题:
(1)判断甲、乙、丙三位同学的多项式是否为“友好多项式”,并说明理由.
(2)丁的多项式是什么?(请直接写出所有答案).
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某种产品,每件产品的生产成本为25元,出厂价为50元.在生产过程中,平均每生产一件这种产品有0.5m3的污水排出.为净化环境,该厂购买了一套污水处理设备,每处理1m3污水所需原材料费为2元,每月排污设备耗费4000元.
(1)请给出该厂每月的利润与产品件数的函数关系式;
(2)为保证每月盈利30000元,该厂每月至少需生产并销售这种产品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.
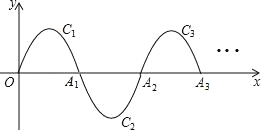
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
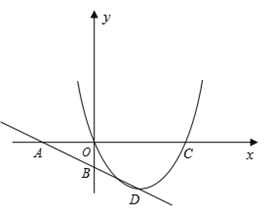
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-2x+1=0.
(1)若方程有两个实数根,求m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2-x1-x2=![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四座城市A,B,C,D分别位于一个边长100km的大正方形的四个顶点,由于各城市之间的商业往来日益频繁,于是政府决定修建公路网连接它们,根据实际,公路总长设计得越短越好,公开招标的信息发布后,一个又一个方案被提交上来,经过初审后,拟从下面四个方案中选定一个再进一步认证,其中符合要求的方案是( )




A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步丰富学生课余文化生活和营造朝气蓬勃的校园文化氛围,学校组织学生开展了各种文体活动、社团活动,现在开展的社团活动有音乐,体育,美术,摄影四类,每个同学必须且只能从中选择参加一个社团,为了解学生参与社团活动的情况,学生会成员随机调查了一部分学生所参加的社团类别并绘制了以下两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
社团活动条形统计图 社团活动扇形统计图


(1)本次一共调查了_____________________名同学;
(2)补全统计图;在扇形统计图中,“美术”所在扇形的圆心角的度数为_______________;
(3)小明和小亮都想报美术,摄影,体育社团,用画树状图或列表的方法,求他们恰好参加同一社团的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求![]() 的值.
的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则![]() =
= ![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则![]() =
= ![]() =111=1;
=111=1;
所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(2)已知![]() =9,
=9,![]() =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com