
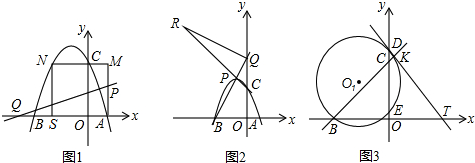
分析 (1)根据正方形的性质得到C(0,3),设点A的坐标是(a,0),根据翻折变换的性质求出m的值,根据待定系数法求出抛物线的解析式;
(2)设点P的坐标是(a,-a2-2a+3),表示出BP所在的直线的解析式和RQ所在的直线的解析式,根据BQ=RQ,列出关系式,运用分情况讨论思想进行解答即可.
解答 解:(1)∵正方形AMNS的边长为3,
∴C(0,3),
设点A的坐标是(a,0),
∵将正方形沿直线y=$\frac{1}{3}x+m$翻折,点A恰好与点C重合,
∴$\left\{\begin{array}{l}{\frac{1}{3}×\frac{a}{2}+m=\frac{3}{2}}\\{\frac{3-0}{0-a}×\frac{1}{3}=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{m=\frac{4}{3}}\end{array}\right.$,
∴m的值是$\frac{4}{3}$;
∴A(1,0),S(-2,0),N(-2,3),
∵抛物线y=ax2+bx+c经过A、C、N三点,
∴$\left\{\begin{array}{l}{a+b+c=0}\\{c=3}\\{4a-2b+c=3}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$
∴抛物线的解析式是y=-x2-2x+3.
(2)存在这样的点P,使得BQ=RQ.
如图2,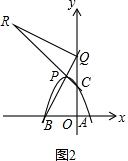 设点P的坐标是(a,-a2-2a+3),BP所在的直线的解析式是y=kx+b,
设点P的坐标是(a,-a2-2a+3),BP所在的直线的解析式是y=kx+b,
则k=$\frac{{-a}^{2}-2a+3}{a+3}$=1-a,
由-3(1-a)+b=0,
解得b=3-3a,
∴BP所在的直线的解析式是:y=(1-a)x+3-3a,
∴点Q的坐标是(0,3-3a),
∴RQ所在的直线的解析式是:y=$\frac{1}{a-1}x+3-3a$,
∵C(0,3),P(a,-a2-2a+3),
∴CP所在的直线的斜率是:$\frac{{-a}^{2}-2a+3-3}{a}=-a-2$,
∴CP所在的直线的解析式是:y=-(a+2)x+3.
联立$\left\{\begin{array}{l}{y=\frac{1}{a-1}x+3-3a}\\{y=-(a+2)x+3}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=\frac{3a(a-1)}{{a}^{2}+a-1}}\\{y=\frac{-{3a}^{3}+9a-3}{{a}^{2}+a-1}}\end{array}\right.$
∵BQ=RQ,
∴BQ2=RQ2,
∴9+(3-3a)2=$\frac{{{9a}^{2}(a-1)}^{2}}{{{(a}^{2}+a-1)}^{2}}+\frac{{9a}^{2}}{{{(a}^{2}+a-1)}^{2}}$,
整理,可得
(a2-2a+2)[${(\frac{a}{{a}^{2}+a-1})}^{2}$-1]=0,
∵a2-2a+2=(a-1)2+1>0,
∴$\frac{a}{{a}^{2}+a-1}=1$或$\frac{a}{{a}^{2}+a-1}=-1$,
①当$\frac{a}{{a}^{2}+a-1}=1$时,
解得a=±1,
∵点P为第二象限内抛物线上一点,
∴a=-1,-a2-2a+3=-1+2+3=4,
∴点P的坐标是(-1,4).
②当$\frac{a}{{a}^{2}+a-1}=-1$时,
解得a=-1±$\sqrt{2}$,
∵点P为第二象限内抛物线上一点,
∴a=-1-$\sqrt{2}$,-a2-2a+3=-(3+2$\sqrt{2}$)-2(-1-$\sqrt{2}$)+3=2,
∴点P的坐标是(-1-$\sqrt{2}$,4).
综上,可得存在这样的点P,使得BQ=RQ,点P的坐标是(-1,4)或(-1-$\sqrt{2}$,4).
点评 本题考查的是二次函数的综合运用、翻折变换的性质,综合运用二次函数的知识、掌握一元二次方程的解法是解题的关键,注意分情况讨论思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
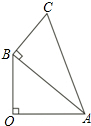 两直角△如图放置,∠AOB=∠ABC=90°,OA=OB=3,点C到OA、OB的距离分别为4,1.将△OAB沿射线OA方向移m个单位(0<m<3),得到新△O1A1B1与△ABC重叠部分的面积记为S,则能表示S与m的函数关系如图象是( )
两直角△如图放置,∠AOB=∠ABC=90°,OA=OB=3,点C到OA、OB的距离分别为4,1.将△OAB沿射线OA方向移m个单位(0<m<3),得到新△O1A1B1与△ABC重叠部分的面积记为S,则能表示S与m的函数关系如图象是( )| A. | 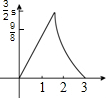 | B. | 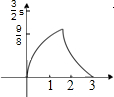 | ||
| C. | 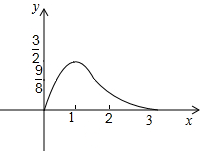 | D. | 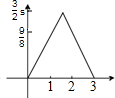 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
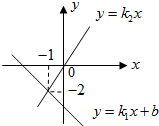 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )| A. | x>-1 | B. | x<-1 | C. | x<-2 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com