
【题目】已知抛物线![]() 经过点A(-1,0),B(3,0)两点,与y轴交点于C(0,-3).
经过点A(-1,0),B(3,0)两点,与y轴交点于C(0,-3).
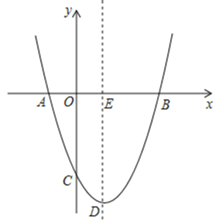
(1)确定该抛物线的解析式,并求出顶点D的坐标;
(2)在抛物线的对称轴上找一点M使得∠AMC=90°,请求出满足条件的所有的点M的坐标;
(3)抛物线上是否存在一点P,使得∠APB=∠ACO ?若存在,请求出P点的横坐标,若不存在,请说明理由.
【答案】(1)y=x2-2x-3,顶点D(1,-4);(2)M(1,-1)或(1,-2);(3)存在,P点横坐标 1+![]() 或1-
或1-![]() .
.
【解析】
(1)由抛物线与![]() 轴的两个交点已知,设抛物线为
轴的两个交点已知,设抛物线为![]() 把C的坐标代入即可得到答案,
把C的坐标代入即可得到答案,
(2)由抛物线的对称轴,设![]() 过
过![]() 作
作![]() 交对称轴于
交对称轴于![]() ,利用勾股定理列方程可得到答案,
,利用勾股定理列方程可得到答案,
(3)以AB为底边,作顶角为2∠ACO的等腰三角形HAB,以H为圆心,HA为半径作⊙H,与抛物线的交点为P,则满足∠APB=∠ACO,对称轴与![]() 交于点
交于点![]() ,求解
,求解![]() 的坐标,利用HP=HA列方程求解即可.
的坐标,利用HP=HA列方程求解即可.
解:(1)![]() 抛物线
抛物线![]() 经过点A(-1,0),B(3,0),
经过点A(-1,0),B(3,0),
设抛物线为:![]()
把C(0,-3)代入得:![]()
![]()
![]() 抛物线为:
抛物线为:![]()
![]()
![]() 抛物线的顶点为:
抛物线的顶点为:![]()
(2)由(1)知:抛物线的对称轴为:![]() 且与
且与![]() 轴交于点E,
轴交于点E,
![]() 设
设![]()
![]()
![]()
![]()
过![]() 作
作![]() 交对称轴于
交对称轴于![]() ,
,
则![]()
![]()
![]()
![]()
![]()
![]()
解得:![]()
![]() 或
或![]()
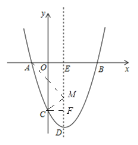
(3)存在点P的坐标使得∠APB=∠ACO成立,
如图,以AB为底边,作顶角为2∠ACO的等腰三角形HAB,以H为圆心,HA为半径作⊙H,与抛物线的交点为P,则满足∠APB=∠ACO,对称轴与![]() 交于点
交于点![]() ,
,
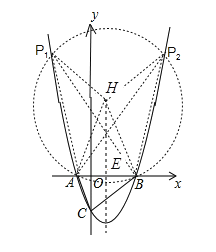
当点H在AB上方时,
![]()
![]()
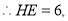
![]() H(1,6).
H(1,6).
设P(x,y),其中![]()
由HP=HA,得![]()
![]()
∴![]()
∴![]()
∴y=0(舍去)或y=11,
由![]() ,
,
解得![]()
∴P点的横坐标为:![]()


科目:初中数学 来源: 题型:
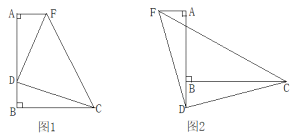
【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小伟一起参加象棋比赛,他们所在的小组共有5名选手.抽签袋里有2红2黑1白共5个小球,摸到同色的成为首轮对手,摸到白球的首轮轮空.现在小组其他3名选手首先依次各摸走一个小球,小亮看到第1个选手摸走的是红球,他对小伟说根据这3名选手的摸球结果我已经知道咱俩恰好首轮对阵的概率了.请你求这个概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
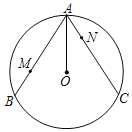
【题目】如图,已知AB、AC是⊙O的两条弦,且AO平分∠BAC.点M、N分别在弦AB、AC上,满足AM=CN.
(1)求证:AB=AC;
(2)联结OM、ON、MN,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑”是中考体育考试项目之一.某中学为了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑的时间的长短依次分为A,B,C,D四个等级进行统计,并绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
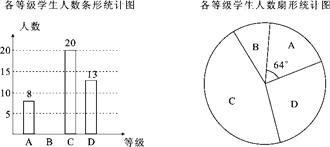
(1)在这次调查中共抽取了 名学生,扇形统计图中,D类所对应的扇形圆心角大小为 ;
(2)所抽取学生“长跑”测试成绩的中位数会落在 等级;
(3)若该校九年级共有900名学生,请你估计该校C等级的学生约在多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
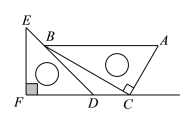
【题目】将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,∠F=∠ACB=90°,AB∥CF,∠E=45°,∠A=60°,AC=8,则CD的长度是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在疫情防控期间,某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液.如果购买100瓶免洗手消毒液和150瓶84消毒液,共需花费1500元;如果购买120瓶免洗手消毒液和160瓶84消毒液,共需花费1720元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)某药店出售免洗手消毒液,满150瓶免费赠送10瓶84消毒液.若学校从该药店购进免洗手消毒液和84消毒液共230瓶,恰好用去1700元,则学校购买免洗手消毒液多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学对一组数据2,3,4,5,5,7进行统计分析,误把3看成了8,则这组数据的计算结果不受影响的是( )
A.平均数B.中位数C.极差D.众数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com