
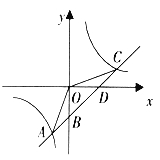
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
(1)求反比例函数![]() 和一次函数
和一次函数![]() 的解析式;
的解析式;
(2)连结OA,OC,求△AOC的面积.
【答案】(1)![]() ;(2)6.
;(2)6.
【解析】试题分析:(1)直接把A点代入反比例函数的解析式求出m的值即可求出其解析式;再根据点C在反比例函数的图象上把点C的坐标代入反比例函数的解析式即可求出n的值,把A、C的坐标代入一次函数关系式即可求出一次函数的解析式;
(2)根据B是直线AC与y轴的交点求出B点坐标,再由S△AOC=S△AOB+S△COB进行计算即可.
解:(1)∵A(﹣2,﹣4)在函数![]() 的图象上,∴m=8,∴反比例函数的解析式为:
的图象上,∴m=8,∴反比例函数的解析式为: ![]() .
.
∵点C(4,n)在函数![]() 的图象上,∴n=2,即C(4,2),
的图象上,∴n=2,即C(4,2),
∵![]() 经过A(﹣2,﹣4),C(4,2),
经过A(﹣2,﹣4),C(4,2),
∴![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为: ![]() ;
;
(2)∵B是直线AC与y轴的交点,∴当x=0时,y=﹣2,
∴点B(0,﹣2),即OB=2,∴S△AOC=S△AOB+S△COB=![]() =6.
=6.


科目:初中数学 来源: 题型:
【题目】我国政府从2007年起对职业中专在校生给予生活补贴,每位在校生每年补贴1500元某市预计2008年职业中专在校生人数是2007年的1.2倍,于是要在2007年的基础上增加补贴600万元。2008年该市职业中专在校生有多少万人?补贴多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据电力部门统计,每天8:00至21:00是用电高峰期,简称“峰时”.21:00至次日8:00是用电低谷期,简称“谷时”为了缓解供电需求的矛盾,某市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:

小明家对换表后最初使用的95千瓦·时电进行测算,发现比在换表前使用95千瓦·时电节约了5.9元,小明家使用“峰时”电和“谷时”电分别是多少千瓦·时?
查看答案和解析>>
科目:初中数学 来源: 题型:
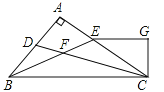
【题目】如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=![]() ∠CGE.
∠CGE.
其中正确的结论是_____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在如图所示的数轴上,把数﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;
(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE,CD分别为其角平分线且交于点O.
(1)当∠A=60°时,求∠BOC的度数;
(2)当∠A=100°时,求∠BOC的度数;
(3)当∠A=α时,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
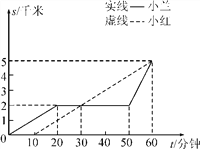
【题目】小红与小兰从学校出发到距学校5千米的书店买书,如图反应了他们两人离开学校的路程与时间的关系.请根据图形解决问题.
(1)小红与小兰谁先出发?早出发几分钟?
(2)小兰前20分钟的速度和最后10分钟的速度各是多少?
(3)小红与小兰从学校到书店的平均速度各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com